Embedding senses via dictionary bootstrapping

텍스트 마이닝 과제를 위한 삽질 중에 시도 중인 논문 정리.

“Embedding senses via dictionary bootstrapping”, Byungkon Kang, Kyung-Ah Sohn. The 33rd Conference on Uncertainty in Artificial Intelligence (UAI), 2017, Sydney, Australia

Click to access 135.pdf

 

TM, NLP의 맥락을 다 보는 무모한 시도를 하다가 반쯤 포기 상태로.. 일단은 제일 기본적인 것들만 보고 그 와중에 강병곤 박사님이 발표하신 논문이 있길래 호기심에 정리. (간만에 연락도..)

일단은 숙제 문제(tweet sentiment analysis)에도 적용이 가능하고, 신경망을 사용한 점도 – 게다가 박사님은 명확한 맥락에서 신경망 기법을 쓰셨을 거라고 기대했기 때문에 정리해보고 가능하다면 구현해보려고 한다. (덧붙여 음악과 관련된 내 연구에도 많은 관점에서 적용될 가능성이 있어서 기대가 된다.)

 

기본 아이디어는 사실 언어문제에 있어서 가장 잘 정제되어 있다고 보면 되는 데이터인 dictionary를 활용해서 word sense disambiguation의 성능을 높이는 시도이다.

 

키포인트: 논문을 이해 못하고 낑낑대다가 간신히 이해해서 적어놓는다! 키포인트를 보자면,

• Dictionary 자체가 훌륭한 labeled dataset의 개념으로 사용될 수 있다는 것.
• 각 단어는 여러 definition sentence를 갖고 있는데, 그 각 definition sentence가 바로 학습을 위한 레이블 같은 역할을 하는 것. (그니까 일단 dictionary 안에서 한 스텝 들어가서 그 안에서 노는 것.)
• 즉, 각 definition sentence가 갖는 ‘맥락’을 이용 -> 그 sentence들을 구성하는 단어들이 갖는 저마다의 (복수의) definition들 중에서 해당 맥락에 맞는 녀석을 고르는 task를 수행하게 함으로써 시스템을 학습시키는 것. (애초의 definition sentence 자체가 어떤 context를 갖기 때문에 그와 최대한 유사한 맥락의 definition을 각 단어에서 고르게 하는 일이 가능하기 때문!)
• Dictionary이기 때문에 가능한 일이다. (어떤 단어에 대한 설명 sentence가 주어지고 그 context가 레이블링 되어 있는 것이나 마찬가지이니까.) 이 학습 과정을 통해서 각 단어(사실 plain word가 아니라 WordNet representation 레벨의 ‘단어’ – 단일 컨텍스트 정보를 포함하는 단위)에 대한 어떤 vector embedding을 이끌어 낼 수 있다.
• 학습은 두가지에 대해 동시에 optimize를 해야 하는 문제가 되는데,
  • v라는 embedding을 구하는 파라메터들(뉴럴넷 파라메터 + simialrity 구하는 파라메터)을 최적화 하는 문제와, 
  • v를 구하는 문제이다.  <- (이 두가지에 대해 명확치가 않아서 질문 메일을 드림..)
• 이에 대해 약간 EM algorithm 비슷하게 번갈아 가며 update를 하게 된다.

 

_Abstract

 

기존의 embedding 모델들은 실제 문장에서 서로 인접하게 등장하는 단어들이 embedding space에서도 가깝다는 단순한 가정으로 학습된다. (Word2vec)

그러나 이런 가정은 중립적이지 않고, 유효하지 않을 수 있다.(corpus에 너무 dependent)

이를 보완하기 위해 우리는 사전(dictionary)을 word embedding을 잘 표현할 수 있는 corpus를 사용했다. -> 단어의 성질을 밝혀낼 때 사전의 definition sentence도 사용해서 동시에 embedding하는 방식

사전은 명확한 sense들의 set을 나열하기 때문에, 이 방식은 semantic한 특징을 반영하는 sense embedding을 제공한다.

 

 

1_ Introduction

 

Word2vec으로 얻은 embedding이 어떻게 유용하게 쓰이는지 소개

(embedding간의 여러가지 연산으로 원하는 값을 얻을 수 있음)

하지만 여러가지 문제가 있다.

• corpora에 너무 dependent 하다 (그 안에서의 co-occurrence만 보니까..)
• out-of-vocab 문제
• sense ambiguity 문제를 무시하는 문제

고로, dictionary를 사용해서 이를 해결해보겠다. (사전은 precise, authoritative description을 포함하니까)

 

dictionary를 사용한 다른 연구도 있었음.

• 기존 word-embedding에 dictionary의 정보를 사용해서 phrase representation을 강화하는데에 사용 / plain word의 여러가지 sense를 구분하지 않음.
• SensEmbed framework: skip-gram이나 continuous bag-of-word embedding 방식으로 개별 sense를 계산 / 하지만 WSD algorithm을 사용한 레이블링을 preprocess단계에서 사용.(정확하다는 보장 없음) -> 반면 우리 방식은 WSD 과정을 embedding 계산 자체에 포함시킨다.

 * 잠만, word sense disambiguation이란 ?

Computational linguistics에서 WSD는 한 word가 sentence에서 어떤 sense로 사용되었는지를 밝혀내는 방법.

우리 방식이 왜 좋은가?

• 작은 사이즈의 corpus로 embedding을 학습할 수 있다.
• Automatic sense disambiguation : 컨텍스트에 따라 여러가지 다른 sense를 갖는 단어들에 대해서 어떤 sense가 문장에 proper semantic을 제공하는지를 파악한다.
• OOV 문제 해결 : 우리는 dictionary를 사용하니까 거기 포함된 단어는 모두 definition sentence가 있다.

 

 

2_Preliminary

 

전체 vocab V : v_1 ~ v_N

각 단어는 d(v_i)={d1i ,d2i ,··· ,dki |dji ∈ O} 와 paired됨. (d(v_i) 는 v_i의 definition string / dki들은 각각이 definition sentence의 어떤 단어)

definition sentence를 구성하는 단어들은 또다른 set O에 속함 (dji ∈ O)

V안의 모든 단어 v_i ∈ V 는 disambiguated 되어 있고, Word Net을 사용해서 표현된다.(w.POS.sense_num 방식)

-> 이 부분이 매우 중요. 즉, 우리의 vocabulary는 w.POS.sense_num 들의 set인 것.

하지만 dji들은 ambiguous하다. (dictionary에 있긴 하지만 아직 disambiguating process를 거치지 않은 것들이니까..)

 

Triple (V, O, d())가 dictionary를 구성한다. dictionary는 closed하다. 즉, definition string에 있는 모든 plain word들은 그 자신 역시 V에 있는 sense들 중에(dictionary에 있는) 하나를 갖는 녀석들이다.

(급Q. 근데 O와 V가 구분되는 이유는 무엇이려나..)

아마도 이것이 이유 -> definition string d(v_i)의 type은 꼭 dictionary definition에 국한될 필요는 없다. as long as v_i를 제대로 설명하기에 충분한 정보만 가지고 있다면. -> Wikipedia article만큼 클 수도 있지만, 이 연구에서는 WordNet definition을 사용. (feasibility 체크를 위해서)

(A. dictionary에 국한하지 않고 더 많은 definition sentence를 확보할 수도 있으니까 O가 더 큰 집합이 될 수 있음 (맞으려나..?))

우리의 목표는 결국 v_i들에 대한 어떤 vector representation을 구하는 것. (dictionary 만을 사용해서) -> dictionary bootstrapping

Our goal is to compute, or refine a vector representation e_i  ∈ R^D for each v_i ∈ V using only the dictionary – hence the name Dictionary bootstrapping.

 

* 잠시, 부트스트래핑?
가설 검증이나 metric 계산 전에 random sampling을 적용하는 방법.(중복허용)
예) 어떤 집단에서 값을 측정했을 때, 그중 임의로 100개를 뽑아 평균을 구하는것
측정된 통계치의 신뢰도 가늠
n개의 데이터 중 중복을 허용한 m개를 뽑고 그들의 평균을 구하는 것을 여러번 반복 -> 평균의 분포 (예를 들어 95% 확률로 sample mean이 어떤 구간에 위치한다는 것을 언급할 수 있다.)

* ML에서의 bootstrapping?
Random sampling을 통해 training data를 늘리는 방법
– 데이터 셋 내의 데이터 분포가 고르지 않은 경우 사용
예) 트레이닝 셋에 사과 이미지 만장 오렌지 이미지 백장이 있으면 항상 사과만 찍는 classifier도 99%의 정확도를 보일 수 있다.(수가 적은 데이터의 error가 무시되는 방향으로 학습..)
이를 해결하기 위해
1) weighting
2) bootstrapping으로 오렌지의 숫자를 늘리는 것
3) 사과 데이터 숫자를 늘리는 것

Overfitting을 줄이는 데도 도움이 된다. (bagging)
: 데이터가 많아야 overfitting이 줄어들지만 그게 어려울 때 사용
: model의 complexity를 줄이는 것은 정확도와 tradeoff
-> ensemble 모델 방식 : 여러 모델의 결과값으로 평균하거나 voting해서 최종값산출 (각각이 biased되어 있어도 평균을 통해 상쇄)

Ensemble 모델을 만들 때, 데이터가 충분치 않아도 bootstrapping을 통해 가능함.
똑같은 알고리즘을 m번 학습시킬 때, 매번 training data에서 random sampling을 해서 구성하면 m개의 서로 다른 모델이 만들어짐.
각 모델은 overfit되어 있을 수 있지만 평균을 냄으로써 어느정도 상쇄시킬 수 있다.

단일 모델의 성능을 높이기 위해서도 사용가능
정확도를 높이기 위해서는 같은 데이터를 반복해서 학습시키는 과정이 필요한데, 단순히 전체 데이터셋을 트레이닝하는 것은 시간이 오래 걸리고 비효율적(충분히 구분되는 데이터에 대해서도 쓸데없이 학습)
-> 각 iteration에 넣을 데이터를 bootstrapping으로 넣어주면 효율적인 학습이 가능하다.

1) n개의 데이터를 추출해서 모델 학습
2) 학습된 모델로 training sample 분류
3) 잘못 분류된 학습 데이터가 샘플링 될 probability를 높이고 잘 분류된 데이터가 샘플링 될 probability를 낮춘다.
4) 다시 n개의 데이터를 추출해서 모델 학습

 

다시 논문으로 돌아와서.

-> word vi에 대한 embedding e를 구하는 가장 직관적인 방법은 vi의 definition, 즉 d(vi)의 embedding을 assign하는 것 (d(vi)는 단어들의 집합임. 즉 definition sentence를 구성하는 word들의 집합) -> 이 d(vi)에 대한 embedding을 구하는 RNN을 학습시키겠다! (우리가 정의한 특별한 RNN을 사용)

The most intuitive way to compute the embedding ei of word vi is to assign the embedding of its definition d(vi).

The embedding of d(vi) is acquired from a recurrent neural network (RNN: Hochreiter and Schmidhuber [1997]). However, we will see in Section 3.2 that such a sequential RNN can be replaced by a simpler RNN. -> 이건 LSTM의 오리지널 논문. 이걸 Message-passing-based RNN으로 대체함.(일단 넘어가자.)

 

 

Q. 그럼 이걸 왜 Dictionary bootstrapping 이라고 불렀을까??

: 트레이닝 데이터에서 계속 샘플링을 해서 less biased된 학습을 유도하겠다는 개념인데, 음.. 우리는 dictionary에 있는 단어들과 그것에 대한 dictionary의 definition sentence를 이용해서 (그것들의 단어들과 그것에 대한 dictionary의 definition sentence를 이용해서.. 이런 식으로 recursive하게) 각 단어 v_i(사실 이건 WordNet representation으로, disambiguated된 의미까지를 포함하는 개념의 ‘단어’)에 대한 어떤 representation을 학습하겠다는 것인데. 이게 somewhat 샘플링하는 것과 비슷한 맥락이라고 볼 수 있는 건가? 혹은, 이것들을 고르는 – 그니까 원래 올바른 definition을 갖는  v와 비슷한 v들을 고르는 과정이 sampling의 개념으로 어렴풋이 비슷한 개념으로 볼 수도 있는 건가. 

아 bootstrapping에서 하는 게 어짜피 그 데이터 풀에서 샘플링을 통해서 가져오는 것인데, dictionary라는 풀에서 가져오는 것과 비슷해서 이런 이름을 사용했을수도.. 아아 나의 이해력이란..

아, 대강 이해를 했다.결국 dictionary에서 먼저 샘플링한 단어들에 대해서 그 단어의 definition sentence들을 이용해서 학습을 위한 input, label 이 형성되는 것이기 때문에, 이 과정이 bootstrapping과 같은 맥락인 것 같다..! (아닐수도)

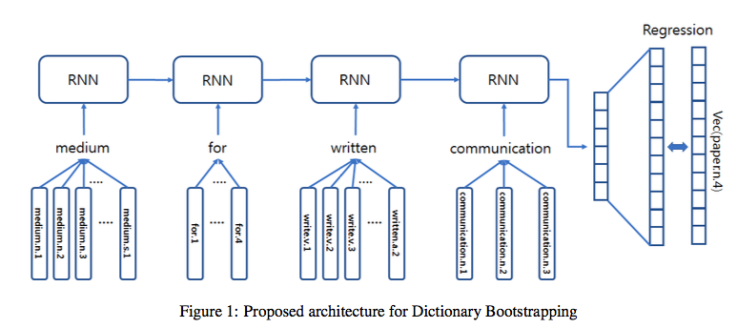
이게 proposed된 구조이다. 그니까 일단 사전에서 찾은 definition sentence를 input sentence 받으면 그 안의 각각의 단어에 대해서 여러개의 v들이 있을 텐데, 이것들을 RNN의 인풋으로 넣고(input sentence의 sequential한 정보도 함께 보게 됨)  이걸 다시 정답 v랑 가까워지는 regression을 통해 학습하겠다는 것. (Q. 그런데 정답 v(이 그림에서는  paper.n.4)는 주어지는 것인가? : 애초에 이 정답 paper.n.4에 대한 definition sentence를 이용하는 것이다. / v가 어떤 vector representation으로 치환되는 과정은 어떻게 이루어지는 것인가? : 더 살펴보자.)

일단 RNN이 학습하는 것은, 어떤 단어의 definition sentence의 각 단어들의 v들을 인풋으로 받아서 정답에 가까운 v(이 v는 그 단어의 v, 혹은 그 단어 자체이기도 함.)를 추론하는 연산. -> 여기까진 명확하다. 이 때, v가 embedding vector e로 옮겨진 후 비교된다? 이 embedding은 어떻게 이루어지는 것인가?

 

 

3_ 알고리즘을 자세히 살펴보장

 

Definition sentence의 plain word를 사용해서 RNN으로 embedding을 뽑아보겠다는 것 (사전에 definition이 명확하게 단어를 설명한다는 가정하에)

One shortcoming of this sequential RNN approach is that we only use the plain words of the definition sentence to derive an embedding.

하지만 임베딩을 input sentence(사전의)의 모호함에 상관없이 잘 뽑아낼 수 있다면 더 좋을 것이다.

 

3_1 resolving ambiguities 

 

각 plain word들을 convex optimization으로 disambiguation한다. (coefficient들을 context에서 뽑아내어서)

-> 즉, 레이블 데이터가 따로 있지 않지만, 어떤 hierarchy 를 갖는 dictionary라는 데이터를 사용해서 convex optimizing 을 통해 disambiguation을 해보겠다는 뜻.

 

어떤 plain word에 대해서 disambiguated word들의 set을 s(d)라고 하면
s(d)는 {v1i, …, vki} 같은 식으로 표현됨.

** 잠깐, 이런 연구에서 WordNet의 definition 사용하는 예
: WordNet을 이용한 알고리즘의 예

• Lesk Algorithm
  http://www.nltk.org/howto/wsd.html
  -> apple.n.1 이런 것들이 무엇을 의미하는지 알 수 있음(synset)
• https://www.inf.ed.ac.uk/teaching/courses/fnlp/Tutorials/7_WSD/tutorial.html
• http://www.nltk.org/_modules/nltk/wsd.html
  -> 이걸보면 단순히 synset중에서 context sentence와 intersection이 많은 녀석을 고르는 알고리즘임을 알 수 있다. (Lesk 알고리즘)

 

(여기서부터 사실 노테이션이 좀 헷깔림 – 앞이랑은 조금 다름? 아님. 다르지 않음..)

• 한 plain word d_i가 있다.
• 그러면 s는 d_i의 모든 disambiguated words들의 set.

예를 들어 s(‘apple’) = {apple.n.1, apple.n.2}  –> 그니까 disambiguated word라는 의미는 WordNet에서의 각 definition key 같은 걸로 치환된다는 뜻 같다. (모든 가능한 disambiguated word들의 set이라는 게 이 key들인지 definition sentence의 모든 단어들을 말하는지는 분명히 모르겠음.)

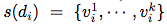
• s(di)를 또한 disambiguated word들에 대응하는 벡터들의 set으로도 사용. (그래서 약자를 v라고 한 것 같기도 하다.)

->그런 다음 어떤 coefficient α를 정의 :  vj가 vj의 컨텍스트와 plain word인 di의 관계에서의 중요도라고 놓는다. (αji : importance of each respective word vj in relation to a plain word di in the context of vj)

• 이 plain word d_i를 다음과 같이 정의할 수 있다.

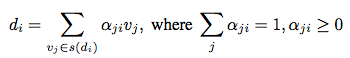
(Q. v_j는 갑자기 어디서 나온걸까. s(d_i)에 속하는 모든 v들이라고 일단 보자. 그러면 각 v_j에 대해서 d_i와의 관계가 얼마나 밀접한지 정도의 개념이 바로 α_ji. 어떤 plain word d_i는 그 단어를 설명하는 v_j들의 합으로 계산될 수 있고, 상황에 따라 α가 달라짐으로써 의미가 달라질 것.)

• vji 의 예시 = apple.n.2 (= d_i ‘apple’의 definition 중 하나)
  모든 단어 v_i ∈ V 는 disambiguated한 애들이고, WordNet 표기를 사용해서 표현된다.(w.POS.sense_num 방식)
• 이런 아이들(w.POS.sense_num)이 어떤 vector representation으로 치환되고 이것들을 사용해서 단어를 벡터화.

(그럼 이 definition들에 대한 벡터화는 어떻게?)

 

α를 확률로 접근하면,

• 각 αij와 vj의(가능한  v들 전부) 곱을 전부 더하면 di의 값이 되고(벡터량)
• 모든 vj에 대한 αij들의 합도 1이 되고
• α는 0보다 크도록 constraint를 둔다.

αji : word d_i가 v_j일 확률

(definition sentence에서 context d-i가 주어졌을 때)

(vi를 제외한 d?)
d-i = {d1,··· , di-1, di+1,··· ,dk}.

αji = Pr(vj|d-i) : 그니까 di를 제외한 word들이 컨디션으로 주어졌을 때 vj의 확률?

  (Q. definition sentence에는 당연히 di는 없을테니 그 안에 있는 word들의 set을 말하는 것이려나? 전체 word set에서 di를 제외한 것은 아닐 것 같으니 일단 그런걸로.)

일단 넘어가면,

그니까 definition sentence들에 있는 단어들이 무엇이냐에 따라서 vj가 무엇인지가 결정된다는 관계성이 정의되는 것이라고도 할 수 있다.

이건 일단 베이즈룰을 써서 일케 정리가 가능하다.

 

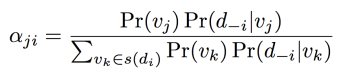
그럼 이 coefficient α를 구하기 위한 과정을 좀 더 풀어보자.

앞부분 prior부터 생각하면,

먼저, 언어에 대한 우리의 existing knowledge를 사용하는 것이 가능하다.

예) 어떤 plain word에 대해 오직 처음 몇개의 sense들이 훨씬 주로 사용되는 것들이라는 등의 사전 지식 -> Pr(vj)가 exp( j ), 즉 순서에 비례하게 한다던지 하는 방식으로 적용

이런 assumption이 적용되지 않으면 단순히 Pr(vj) = |s(di)|^(-1) 이 적용된다. (s(di)는 disambiguated word들의 set인데 이들의 수 분의 일이니까 단순히 uniform distribution)

 

이제 Pr(d_-i|vj)을 구해야 하는데, 이를 위해 d_-i에 있는 plain word를 observe할 확률들이 서로 conditionally independent하다는 가정을 한다. (vj가 주어졌을 때 각각 word들은 independent)

(-> 이걸 보면 결국 d_-i는 실제 definition sentence를 말하는 것 같고.. 그 안에 있는 개별 단어들의 확률이 CI라는 가정을 하는 것 같음.)

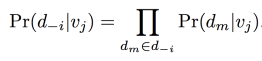
그러면 단순히 모든 단어들의 확률의 곱으로 Pr(d-i|vj)를 구할 수 있다.

그럼 각 단어의 확률 Pr(dm|vj)는 어떻게 구할까?

이 식을 잘 헤쳐보장.

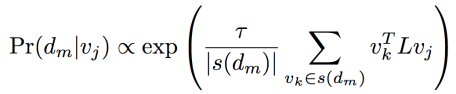
definition key vj가 주어졌을 때 definition sentence에 각 단어 dm이 있었을 확률은

: dm에 대한 모든 disambiguated word들의 set인 vk들에 대해서 vj와의 similarity를 평균낸 것이다. (이것이 key idea 중 하나인듯)

-> 벡터간의 내적이 둘의 유사도의 한 형태이고,  positive semi-definite 정방 행렬 A가 있으면 ‘내적’의 개념을 일반화 할 수 있음 (x^TAy. 이 경우, A 행렬은 x와 y 의 성분들 간의 연관성을 새로이 정의하는 역할. A가 항등행렬 이면 원래의 내적.)

그래서 x와 y의 새로운 유사도를 정의하기 위해 A를 학습하는 방법을 많이 취하는데, 이게 metric learning의 핵심.

 

Pr(dm|vj)를 average of similarities between vj and the senses of dm(vk들)로 나타내는데, L이라는 parameter가 사용된다. (DxD dimension의 실수 param)

(타오는 아마  노말라이져 정도이려나?)

이 inner product가 유효하도록 하기 위해 우리는 L이 positive-definite하다고 제한한다.

* positive definite : symmetric한 매트릭스 중에, 임의의 벡터 z에 대해 zTMz의 곱연산을 했을 때의 결과 스칼라 값이 양수가 되도록 하는 매트릭스. (예를 들어 identity 매트릭스는 zTMz 연산의 결과의 모든 항들이 제곱항이 되게 하기 때문에 positvie definite하다.) positive definite matrix의 모든 eigenvalue는 positive하다. Symmetric matrix의 모든 pivot이 positive하면 그 matrix는 positive definite하다.

이 방식은 우리는 사람들이 사전에서 새로운 단어를 look up하는 방식에서 모티브를 얻은 것이다.

새로운 ambiguous word w를 sentence S에서 발견했을 때, 우리는 w의 여러 sense중에서 선택해야 한다. 우리 방식은 w의 sense definition과 S의 plain words와의 비교를 통해서 이를 선택한다. (definition을 직접사용하는 대신 sense embedding을 사용)

Our approach can be thought of as a simplification of this process(여러 sense들 중 선택하는 과정) where we use the sense embedding instead of directly using the definitions.

파라메터(L을 말하는 듯)를 학습하기 위해서는 supervised signal이 필요하다.

 

-> 여기서부터는 그럼 v_i를 어떻게 구하냐는 부분 같음. v_i를 실제로 구하는 것은 아니고, classify 또는 regression을 통해서 비교만 하겠다는 것 같다. (v_i들은 apple.n.2 이런 애들..)

 Q. 그니까 사실 v_j 와 v_k들의 비교를 위해서는 이것들이 어떤 space에서의 벡터량을 가져야 하는데 이걸 어떻게 도출하는지가 의문이다..

 

Classification layer를 RNN의 끝에 달아서 disambiguated word(지금 보고 있는 definition sentence의)를 예측하도록 할 수 도 있지만, 데이터가 부족하기 때문에 현재 definition에 따른 단어를 예측하는 classifier는 제대로 된 것이 없다.

각 class(즉, 각 단어..)에 대해서 하나의 데이터 포인트(definition embedding)가 있을 뿐이기 때문이다.

따라서 대신에, 우리는 regression을 통한 supervised signal을 사용하고자 한다.

각 단어 vi ∈ V 들과 이들의 definition embedding e_i(? 이걸 모르겠음)에 대해서, u_i가 v_i의 현재 embedding이라고 하면, 우리 objective는 어떤 (non-linear) function을 학습하는 것이 된다. -신경망

이 함수는 e_i를(D dimension) 인풋으로 받아서 u_i를(역시 D dimension) 만들어 내는 함수. 이 함수를 2개층으로 이루어진 신경망으로 구성하겠다(!) (각 layer weight들을 {W1, W2}라고 노테이트 / 여기에 L1 regularization 텀을 더함)

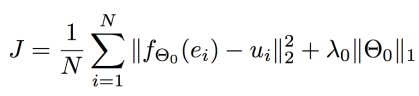
-> 그니까 sentence의 어떤 단어의 v_i에 대해서 그 definition embedding e_i를 신경망에 통과시킨 아웃풋과 v_i의 current label embedding u_i의 차이가 cost가 되고, L1 term을 더한 것.

이렇게 해서 v_i를 근사하겠다는 것.

잠깐,  그럼 일단 정답 u_i들이 있어야 하는 것 아닌가?  주어진 sentence에서 정답이었던 u_i들에 레이블로 주어진 데이터가 필요할것 같은데 흠..  그런데 뒤에 experiment 섹션을 보면, 사용한 training corpus는 WordNet 데이터가 유일하다고 했다. WordNet의 단어들과 그 definition들. -> 이 부분은 이해했음. 애초에 특정 v 자체에 대해서 시작한 것이니까 그게 ‘current label embedding u_i’를 갖는 v였던 셈이다. 단지 v_i -> u_i 이 vectorization을 아직 모르겠을 뿐..

Experiment 섹션을 잠시 먼저 보자.

English Wikipedia corpora에서 가장 빈번하게 등장하는 10000개의 plain word를 가져와서 ‘seed word’로 사용했다. 이 시드 워드를 사용해서 WordNet에 없는 애들은 prun하고, WordNet definition을 traverse(트리 traverse하듯이..)했다. 이 때 새롭게 등장하는 (10000개 중에 없었던) 단어들이 sense에서 발견되면 vocabulary에 추가했다. 또한,  definition에서 3번 미만으로 사용된 단어들도 제거했다.

-> 이걸 보면 dictionary (즉, WordNet)에서의 단어들 사이의 co-occurrence를 key relationship characteristic 정도로 사용했다는 것 같다.(TF-IDF 같은 거 구할 때에도 저런 식의 느낌으로 제거하고 하니..) -> 즉 dictionary 자체에서 word들의 특징을 잡아 내고, 이를 단어의 embedding으로 활용했다는 것 같다. 이 맥락을 유지하면서 다시 내용을 살펴보자.

 

• 다시 정리해보면,  애초에 우리가 알려고 했던 값은 α : 즉, 주어진 단어에 대한 WordNet에서의 definition sentence의 candidate들 (이것 하나 하나가 벡터) 각각의 확률값.
• α를 확률로 정의하고 이를 구하기 위해 definition sentence안의 어떤 단어 dm에 주어졌을 때 vj가 assign될 확률을 구함 (Q. definition sentence는 어떨 땐 vector이고, 여기선 또 sentence인데, 이 구분이 약간 헷깔림.)
• 이를 베이즈룰로 정리해서 vj가 주어졌을 때의 각 dm의 확률로 바꾸어준 뒤,
• 이 시점에서 (recursive느낌으로 한 스텝 들어가서) dm을 정의하는 vk들의 모든 set에 대해서 average한 값이 vj와 비슷해지도록 optimize
• 이 optimizing을 위해서 cost함수를 정의한 것이 바로 위에 나온 함수 – 즉, dictionary안의 definition sentence를 구성하는 단어 dm에 대한 설명들인 vk들을 실제 이들의 embedding인 ui와 가깝게 만들어주는 optimization.

 

이를 위해 아까 classification layer를 더하는 방식은 취하했지만, 데이터가 많다면 그 방식도 유효할 것이라고 생각한다. 예를 들어, 우리가 WordNet resource를 자유롭게 사용하고자 했다면(혹은 자유롭게 사용할 수 있었다면?), 우리는 class structure를 좀 더 word semantic hierarchy를 반영하는 구조로 reformulate할 수도 있었을 것이다. (Q. WordNet resource는 자유롭게 사용할 수 없는 것인가?)

물론, 일반적인 sentence들은(나중에 어떤 식으로든 적용할 문제에 나올 sentence들) 어떤 단어에 대한 definition은 아닐 것이다. 하지만 이렇게 word-definition pair를 학습해서 얻은 sentence들을 사용해서 알고리즘이 올바른 semantic을 배울 것이라고 기대한다. (그러므로 적용 가능할 것이다.)

 

 

3_2 Message-passing-based RNN

 

(아마도 이 섹션이 지금까지의 의문 –  ‘임베딩 vector를 어떻게 구할 것인가’에 대한 답인 듯 하다.)

이론적으로는 definition embedding e_i를 v_i에 바로 assign하는 것이 맞는 것 같다.

이 procedure는 converge하기까지 fixed-point iteration procedure (v_i <- e_i)을 반복하게 된다. 그러나 경험적으로 좋지 않은 embedding에 converge한다는 것을 알았다. 이는 RNN 학습과정이 v_i를 너무 초보적으로 다루기 때문이다. : RNN은 문장의 한 plain word마다 각 sense들의 convex combination을 취하기 때문이다. (아직 이 sense들이 converge하지 않은 상태에서)

또한 random initialization도 이 상황을 악화시킨다.

 

** fixed-point iteration

 

 

이 문제를 해결하기 위한 definition embedding form을 제시한다. (문제 해결 및 파라메터 숫자 감소) -> word가 속한 클러스터링과 coordinate를 찾는 일을 동시에 하는 것이다.

이에 대한(이렇게 동시에 하는) 기존 방법은 manifold learning algorithm (multi-dimensional scaling(MDS)) 이나 locally-linear embedding(LLE) 같은 것들이다. 하지만 이런 방식은 pairwise distance가 필요한데 우린 갖고 있지 않다..

대신에 우리는 한 단어의 embedding이 그 단어의 definition sentence에 있는 단어들에 영향받는 방식의 모델을 만들었다.

좀더 자세히는, definition sentence의 plain word들의 linear combination으로 disambiguated word embedding을 업데이트한다는 가정으로 linear influence model을 만들었다.

: a linear influence model where the plain words in the definition are linearly combined to update the corresponding disambiguated word embedding.

우리 모델은 단어들의 doubly-convex combination를 취하는데, 첫번째 level은 plain word를 어떤 pre-computed weight에(h_d) 따라 combine하고, 두번째 level은 각 plain word의 disambiguated word들을 combine한다.

아래 그림을 보며 이해해보자..

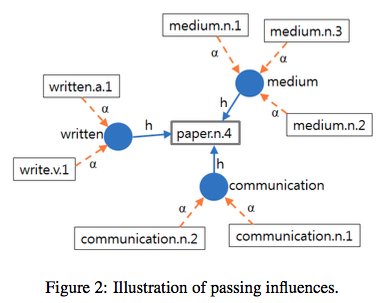
그니까.. 이처럼 각 v_i에 대한 이런 recursive form을 갖게 된다 :

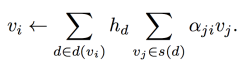
h_d : plain word weight (d(v_i)에 있는 모든 plain word 들 각각의 weight)

(왜냐하믄, 기억하는가?

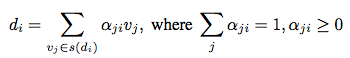
이렇게 정의했으니까.)

 

그니까.. paper.n.4를 예로 들자면, v_i (즉, paper.n.4)는 d_-i의 각 단어들의 weighted sum이다. 근데 그 각 단어들도 각자 본인의 definition들인 v_j들의 weighted sum이다.

이 plain word weight h_d는 각 v_i에 대해서 pre-computed / normalized 되어서 constant로 사용됨. (The plain word weights h_d are normalized for each disambiguated word vi, and can be pre-computed as constants.) -> Inverse-document frequency(IDF)의 접근으로 이걸 precompute 했다! (다른 weighting scheme도 가능하다.)

 

Intuitively, words that are defined using similar words (i.e., words with similar meaning) will have higher chance of receiving and passing influences among themselves, and hence result in closer embedding.

-> 직관적으로 보자면, 비슷한 단어를 사용해서 정의된 단어들은 (즉, 비슷한 의미를 지니는 단어들은) 그들 사이에 영향력을 주고 받을 확률이 더 크고, 따라서 embedding space에서 더 가까워 진다는 개념이다.

 

이를 그래피컬 모델 측면에서 보자면 dictionary 안의 모든 단어들로 이루어진 그래프에서의 belief propagation algorithm을 연상시킨다.

Plain word들과 disambiguated word들이 vertex set을 구성하고, plain word는 disambiguated word로 부터 directed edge를 receive하고, disambiguated word는 본인의 definition sentence에 속하는 plain word들로 부터 directed edge를 receive한다. 이때 edge의 weight들이 h_d, α_ji 인 것이다.

이 관점에서 계속 보자면, v_i를 업데이트하는 양은 variable node들로부터의 log-message들이 모두 sum up된 것과 같다. (message에 로그씌운 것을 의미하는 듯)

불행히도 이 그래프는 트리구조가 아니기 때문에 update가 converge한다는 보장이 없다. 따라서 다음 measure를 이용해서 보완한다.

• Β_t ∈ (0, 1) 이라는 파라메터를 정의.
• Β_t는 각 iteration epoch t마다 변화하면서 다음 수식의 balance를 맞추는 역할을 한다. (수식에서 update와 stabilization 사이의 균형을 맞추어 줌.)

 

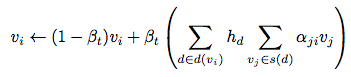
Β_t가 높으면 message-passing encoder로부터 받는 update를 더 공격적으로 받아들이고, Β_t가 낮으면 보수적으로 기존 v_i의 값을 더 유지하려고 한다.

학습을 진행하면, 먼저 높은 Β_t 값으로 시작해서 시간이 흐를수록 낮추어 준다. (이렇게 낮춤으로써 자연스럽게 converge가 보장됨.)

 

• 정리하자면 이 업데이트 방식은 random walk 기법의 unnormalized version이라고도 러프하게 볼 수 있다. (각 단어가 자신에 대한 definition을 구성하는 plain word들로부터 영향을 받는 구조.) Outgoing influence들의 총합이 1이 되지 않기 때문에 ‘unnormalized’라고 불렀다.
• Random walker는 unnormalized된 영향력을 neighbor들에 전파한다.
• 그러면 비슷한 단어를 사용하는 단어들은 대강 비슷한 influence를 받게 되고,
• 대략적으로 semantic한 clustering이 이루어지는 것이다.

 

_Simplified RNN

• 이 message-passing-based update는 simplified RNN에서의 computation이라고도 볼 수 있다.
• 이 RNN은,
  • identity activation function 사용. (이런게 있었단 말인가..?)
  • 단순히 accumulates the inputs (input들의 순서는 무시) (이게 RNN인가..?)
• Bag-of- words (BOW) neural language model 이라는 모델에서 사용했던 RNN 방식이다. (있었구나..)
• 너무 sentence를 날것 그대로(..) encode하는 것처럼 보이긴 하지만, 짧은 sentence를 encoding 할 때에는 효과적인 방식이다.
• 우리의 definition sentence들은 대부분 phrase-level의 표현들이기 때문에, 이 BOW방식을 사용하는 것도 정당화 될 수 있다!..

 

 

3_3 Overall Training

 

우리 word-embedding 기법은 2개의 phase로 이루어짐.

• Regressor training phase
• Message-passing-based update phase

-> 이 둘이 연결되어 있어서 한 phase에서 업데이트 된 variable들이 나머지에서 constant로 사용됨. -> alternating training scheme 사용

 

1) Training the regressor

• disambiguated word vector v_i들을 freeze
• parameter 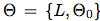 를 업데이트.
• 이상적으로는 RNN을 converge할 때까지 학습해야겠지만, K round만 먼저 학습
• 즉, SGD로 L_1 을 k번 업데이트

2)  Message-passing-based update

• 여기에 더 많은 시간을 할애함. (이런 fixed-point iteration이 상대적으로 더 빨리 converge하기 때문)
• 이 iteration은 previous value와 updated value의 maximum 차이값이 임의의 threshold ε 보다 작아지는 때에 멈춘다.
• 이 업데이트는 ‘in-place’하다. 즉, 새로운 값이 바로바로 업데이트 된다. (batch update까지 기다리지 않고) -> 업데이트된 값이 바로 사용됨으로써 더 빨리 converge할 수 있음.

 

<업데이트 알고리즘>

 

 

3_4 Extension with base vectors

 

지금까지는 v_i에 대한 업데이트가 오로지 neighbor들을 사용한 함수로만 이루어졌다. 이 섹션에서는 이런 scheme에 좀 더 generalized된 extension을 더해보고자 한다.

-> v_i에 대한 업데이트에 pre-trained된 vector b_i를 추가로 사용.

아까 정의한 update식에 다음과 같이 항이 추가된다.

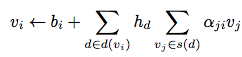
• b_i : base vector (이 벡터가 base representation을 제공)
• 이건 pre-trained 되어서 제공된다.
• 각 definition을 하나의 짧은 document라고 생각하고 topic modeling을 적용. -> 각 단어의 topic distribution을 계산. (LDA with k topics를 구하면 각 단어에 대한 k-dimensional probability vector를 얻을 수 있음.)
• 이 topic vector를 사용해서 임의의 두 word사이의 여러가지 distance metric을 구할 수 있음. (Bhattacharyya distance 또는 Jensen-Shannon distance 같은..)
• 이 distance를 N x N matrix로 구성해서 MDS(multi-dimensional scaling)의 인풋으로 넣음.
• 이 matrix에 대해 MDS를 수행한 결과가 바로 각 단어의 vector representation이 되는데 이는 다른 단어들로부터의 거리를 반영한 vector가 되는 것.
• 이렇게 얻은 vector가 best representation은 아닐지 몰라도, 적어도 우리 방식에 활용할 initial value로써 훌륭할 것으로 기대한다.
• 이 방식은 definition sentence들이 짧을 경우에 더 잘 작동한다. (만약 아닐 경우, 짧은 text에 특화된 topic model을 적용해도 좋을 것이다.)
• 섹션 3_5에서 이 초기화 scheme이 더 유용하게 사용되는 시나리오를 설명할 것이다.

 

 

3_5 Applications

 

이 방식이 사용될 수 있는 application을 알아보자.

 

1) Word sense disambiguation

• 주어진 임의의 sentence를 우리의 RNN 모델에 넣고,

• 원하는 단어 w에 대해 올바른 sense를 알고 싶으면 계산된 α_wj 를 보면 된다.

-> 이걸 보면 RNN으로 얻은 결과에서 α를 알 수 있다는 것 같은데..?

Disambiguating plain words involves comparing each of the senses to the surrounding words in the context. This is exactly how our model operates to assign weights on the senses. (RNN모델이 sense에 대해 weight을 assign 하는 일을 하는 거였구나..)

 

2) Out-of-vocabulary embedding

• 대부분의  word embedding들은 co-occurrence pattern에 매우 의존해서 계산된다. -> 잘 co-occur하지 않는 단어들이나 새로운 생겨난 단어들은 embedding을 계산할 컨텍스트가 부족하게 된다.
• 반면 우리의 embedding 모델은 사전에 definition이 있는 단어라면 embedding을 계산할 수 있다.  (In fact, a closed set of related definitions is the minimally required information to learn the meaning of a new word.)
• 알려지지 않은 단어에 대한 embedding을 구하는 것도 단순하다. 그 단어의 definition을 RNN에 넣고 α_ji들을 계산한다. 그리고 나서,

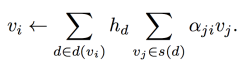
이 과정을 한번 계산해서 v_i를 구하면 된다.

 

3) Encyclopedia embedding

• 지금까지는 제한된 정보라고 볼 수 있는 dictionary를 사용했다.
• 그리고 definition 이 sentence 형태라고 가정했다.
• 하지만 사전 말고도 훨씬 풍부한 정보를 가진 resource들을 사용할 수 있다.
  •  Wikipedia
    • multi-sentence, multi-modal definition
    • entry들이 hyperlinked되어 있기 때문에 우리의 random walk framework가 local한 iterative algorithm이 될 수 있다.
    • 즉, hyperlinked된 환경에서는,

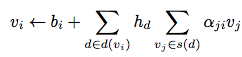
이 수식을 Bellman equation 이라고 생각할 수 있다. (강화학습에서처럼 선택지에 따라 recursive하게 들어가는 구조에서 reward를 추정하는..)

: 즉 b_i가 페이지 i의 컨텐트를 나타내고, h_d와 α_ji들이 합쳐져서 random walk (페이지 i로 부터 neighbor 페이지들인 j들로 가는) 확률이 되는 것이다.

• 그렇다면 먼저 entry document에 대한 embedding을 어떻게 할 것인가에 대한 부분이 남는데, 이는 우리가 다뤄왔던 한 sentence에 대한 처리와는 많이 다르다. -> multi-modal embedding 테크닉을 사용해서 document에 대한 summary vector를 추출해야 할 것이다. -> 하지만 추측컨데, 이 document들은 하나의 컨셉에 매우 focused된 녀석들이기 때문에 충분히 high-dimensional한 vector를 사용하면 잘 작동할 것이다.

 

 

4_Experiments

 

• qualitative
• quantitative

 

_데이터 준비

English Wikipedia corpora에서 가장 빈번하게 등장하는 10000개의 plain word를 가져와서 ‘seed word’로 사용했다. 이 시드 워드를 사용해서 WordNet에 없는 애들은 prun하고, WordNet definition을 traverse(트리 traverse하듯이..)했다. 이 때 새롭게 등장하는 (10000개 중에 없었던) 단어들이 sense에서 발견되면 vocabulary에 추가했다. 또한,  definition에서 3번 미만으로 사용된 단어들도 제거했다.

->

|V | = 82, 831 words

|O| = 38, 730 plain words

 

WordNet의 단점 : 4개의 POS중 하나인 단어들에 대해서만 definition이 제공된다는 제한이 있음. -> stop-words (prepositions, conjunctions, articles 들)은 main vocabulary에서 제외됨.

한 문장의  semantic을 해석함에 잇어서 stop-word들이 중요함에도 불구하고 이 연구에서는 이를 무시하기로 했다. 왜?

• 제한된 vocabulary에서도 얼마나 embedding을 잘 배우는지 보이고 싶었다.
• stop-word를 vocabulary에 모두 포함시키는 작업은 매우 복잡한 pre-, post- processing이 필요하기 때문이다. (우리는 사전이외에 어떤 linguistic/textual resource를 사용하지 않았다.)

 

파라메터 들에 대한 명세는 다음과 같다.

 

4_1 Qualitative Results

 

 

 

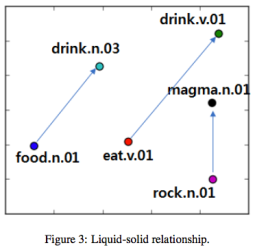
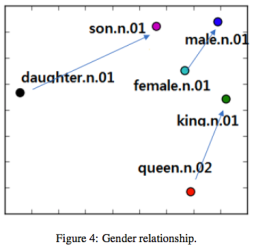
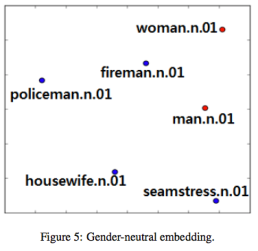
4_2 Word sense disambiguation Results (Quantitative)

 

 

 

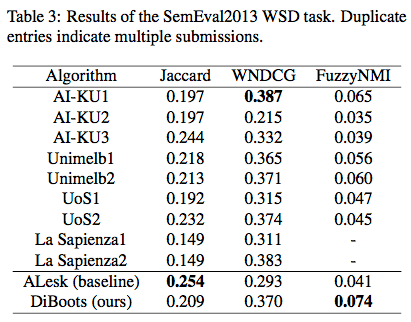
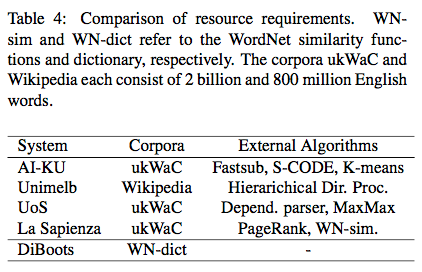
5_ Discussion

 

• Task에서 SOTA 성능을 보이지는 못했지만,
• 6.9MB의 dictionary만을 사용했다는 면에서 매우 좋은 성능이라고 볼 수 있다.
• 또한 simple case-lowering외에 어떤 text processing을 더하지 않았다.

 

우리 모델을 개선할 수 있는 방향은 크게 두가지

• Language processing
  • POS tag, 시제, number, compound noun을 무시했지만, semantic을 밝히는 데에 매우 중요한 것들이다. 또한 conjunction, preposition도 무시했다.(WordNet의 한계) 이런 것들을 모두 끌어들이는 방식으로 개선할 수 있다.
• 기존 embedding과의 결합
  • Table 2에서 볼 수 있듯이 apple.n.1의 가장 가까운 이웃들은 모두 valid한(..)  apple들이지만, 일반 사람들에게 잘 알려지지 않은 것들이다. GloVe 같은 embedding은 좀더 user-friendly 한 단어들을 제공한다. (naturally co-occurring하는 word들에 기반한 embedding이기 때문) 우리 알고리즘(DiBoots)이 더 정확한 단어를 제공하긴 하지만 일반인들에게는 잘 안 맞을 수 있다. (사전에서 정확한 semantic을 가져오는 게 사람들이 기대하는 것과 다른 경우가 많다는 뜻이기도 하다..)
  • 따라서, 우리의 알고리즘으로 기존의 embedding을 fine-tuning하는 것도 좋은 combination이 될 것으로 보인다.