GAN tutorial 2016 정리(1)

GAN tutorial 2016 내용 정리.

https://arxiv.org/abs/1701.00160

GAN tutorial 2017 (https://nips.cc/Conferences/2016/Schedule?showEvent=6202) 이 나온 마당에 이걸 정리해본다(..)

_소개.

Generative model들중 어떤 아이들은 density estimation을 통해 generate한다. (like variational inference autoencoder)

어떤 data-generating distribution(p_data)에서 트레이닝 데이터를 샘플링한 후, distribution의 estimation을 계산하는 것.

그니까 true(optimal한) density가 되기 원하는 p_model(x)를 estimate한다는 이야기.

예를 들어, 실제 이미지들을 가지고 학습한다면, 그 이미지들을 fit하도록 학습(estimate)한 distribution에서 샘플링을 하면 비슷한 (있을법한) 이미지가 생성된다는 원리이다. (ideally는 그렇다는 뜻, 실제로는 아직 그렇게 하지 못한다.)

GAN도 이런 원리를 따르는 generative model중 하나이다.

• 이를 위해 아예 명시적으로 p_model을 estimate할 수도 있고, (MLE)
• 혹은 p_model을 통해서 sample generation만 하기도 한다.

(-> 사실 GAN은 sample generation에 우선적으로 집중하지만, 둘다 하도록 할 수도 있음.)

1_ Why generative model?

시작전에 generative model 학습을 통한 장점들을 살펴보자.

• High dimensional prob. distribution을 추출해서 다룰 수 있게 됨.
• Reinforcement learning 에서 model-based model들은 generative model을 포함한다. (sequential한 데이터에 대한 generative model은 미래의 데이터를 예측할 수 있게 해줌.)
• Semi-supervised learning에서 활용될 수 있다.

아래 예시를 보자. 비디오의 다음 frame을 예측하는 모델이다.  loss에 MSE를 사용하면 귀와 눈이 blurry해지는 것을 볼 수 있지만, GAN은 sharp하게 generate함을 알 수 있다. (좀 더 세밀해진다.)

이는 ‘GAN loss’를 사용함으로써 여러 possible output 중에서 어느 녀석이 더 디테일하고 실제와 가까운 이미지인지 판별할 수 있게 되었기 때문에 가능한 일이다.

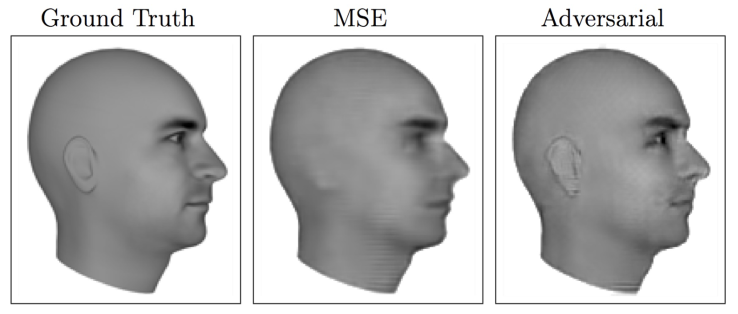
GAN은 multi-modal 한 output을 다루게 해준다. 따라서, Input은 사실 여러 다양한 ‘correct'(acceptable) answer를 가질 수 있지만 이 중에 더 세밀하게 맞는 것을 학습하도록 하는 역할을 한다.

2_ How generative models work, and how is GAN different?

2_1 MLE

일반적으로 generative model들은 maximum likelihood로 학습된다.(다 그렇지는 않다.)

어떤 model(probability distribution)을 estimate한 뒤에 maximum-likely한지를 따지는 loss function을 사용하는 것.

-> m개의 주어진 sample에 대해서 가장 likely한 probability distribution을 찾아내는 것.

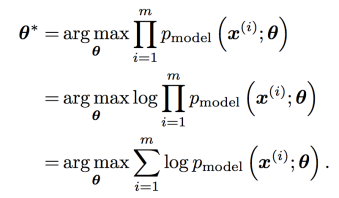
-> optimal parameter 찾기(여러 편의를 위해서 log prob.를 사용한다.)

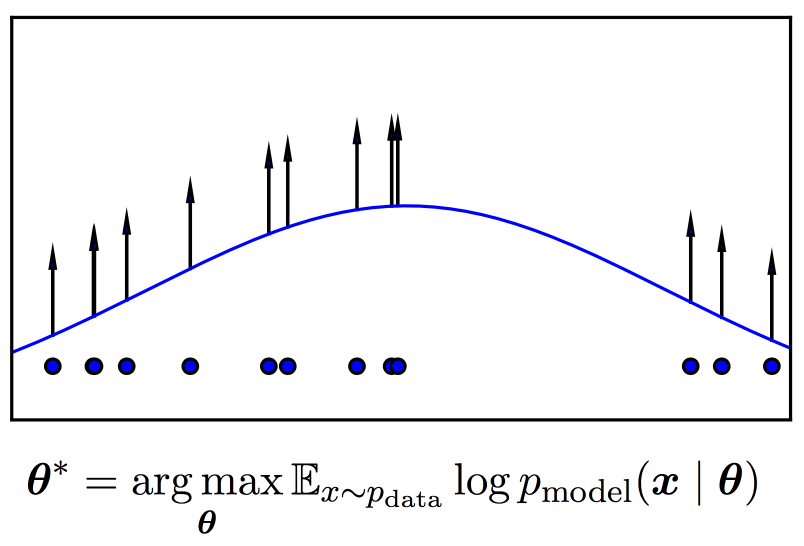
그림처럼 결국 p_model distribution의 기대값을 최대화하는 (model의)parameter를 찾아내는 것이다.

Maximum likelihood estimation을 구하는 방법으로는 실제 data generating distribution과 model과의 KL divergence로 구하는 방법이 있다.

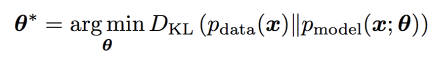
만약 p_data가 p_model의 family distribution에 속하면, model은 p_data를 정확히 재현할 수 있다. (여기서 말하는 family distribution이 exponential family를 말하는 것인지는 정확히 모르겠음.)

(하지만 물론 실제 문제에서는 true p_data를 알 수 없고, training set(m개의)으로 추정한 approximate p_data를 사용하는 것이다.)

이 KL divergence값을 최소화한다는 것이 결국 training set의 log-likelihood를 최대화한다는 것이 됨.

 

2_2  Taxonomy of deep generative models

이러한 ML 문제를 명시적으로 푸느냐, implicit하게 푸느냐에 따라 방법론이 나뉜다.

likelihood를 어떻게 represent하느냐(혹은 approximate하느냐)에 따라 다음 그림과 같이 분류를 나누어 볼 수 있다.

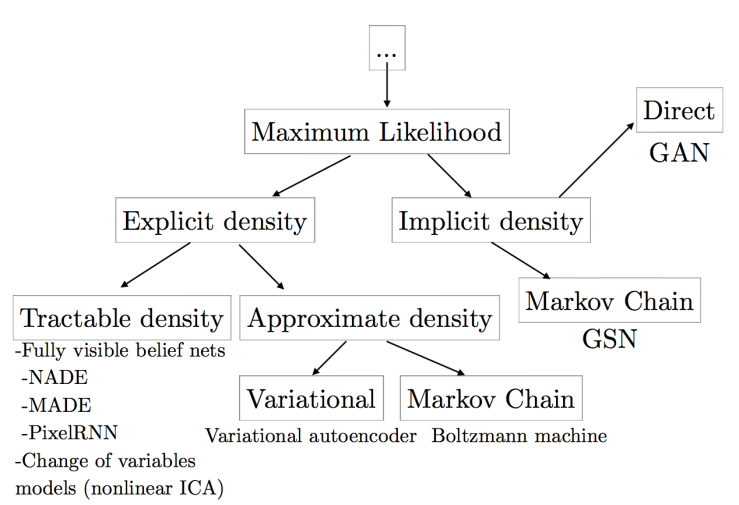
왼편은 p_model의 density를 explicit하게 정의하는 쪽이다. 계산이 tractable하기도 하고 intractable하기도(이경우 variational기법이나 sampling 기반 기법(MCMC같은)을 사용) 하다.

오른편은 p_model을 명시적으로 정의하지 않고, 어떤 인터랙션을 갖는 관계를 정의한다. 일반적으로 이 distribution에서 얻은 샘플을 가지고 인터랙션을 설정한다.

• 이들 중 어떤 모델들은 Markov chain등의 sampling 기반 기법들을 사용한다. (sampling을 하는 왼편의 모델들과 다른 점은 model 자체에 대한 approximation이라는 점.) : model은 주어진 sample들을 확률적인 의미를 갖도록 변환해서(어떤 distribution으로) 새로운 sample을 얻을 수 있도록 한다.
• 다른 모델들은(GAN같은) input data없이 한 step에서 하나의 sample을 generate한다. (GAN의 트레이닝 과정을 보면 density를 정의하지 않고 generation에만 활용한다.) Implicit한 모델로부터 distribution을 만들고 이로부터 sample를 바로 생성하는 것.

GAN은 여러 모델들의 단점을 보완하기 위해 만들어졌지만, 물론 본인만의 단점도 있다.

2_3 Explicit density models

왼편의 모델들부터 살펴보자.

p_model을 명시적으로 정의하기 때문에 ML이 straightforward하다. 모델의 정의를 가지고 likelihood를 정의하고 gradient로 최적화하면 된다.

하지만 complex한 data에 대해서 computationally tractable한 모델을 정의하는 작업이 쉽지 않다. 이를 위해,

• tractability를 유지하면서 carefully 정의하는 법
• tractable approximation이 가능한 모델을 정의하는 법

두가지 방법으로 나뉠 수 있다.

 

2_3_1 Tractable explicit model

가장 왼편의 방법들은 density function을 explicit하게 정의한 방법들이다. (careful하게 정의..)

• fully visible belief network
• nonlinear independent component analysis

_Fully visible belief network(FVBN)

FVBN은 확률의 chain rule을 사용해서 n-dimensional vector x를 one-dimensional probability distribution으로 decompose하는 방법이다.

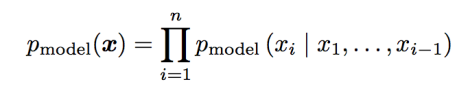
(샘플링 기반 inference에서의 방법론과 비슷.)

(참고로, FVBN / GAN / VAE 세가지가 가장 popular한 방법이다. )

여기서 DeepMind의 WaveNet에서와 같은 세련된 방법을 사용하는데, 장애가 되는 부분은 sample들이 한번에 하나씩 generate되어야 한다는 부분이다. (x1 다음 x2 같은 식으로..) 따라서 한 sample에 대한 계산량이 O(n)이다.

WaveNet과 같은 modern FVBN에서 xi에 대한 distribution이 deep neural network에 의해 계산되기 때문에, 각 step은 nontrivial한 계산량을 필요로 한다. 게다가 이 step들은 parallel하지 않다. (그래서 WaveNet은 1초의 오디오를 위해 2분의 계산량을 필요로 함..) 이에 비해 GAN은 모든 x가 parallel 하게 generate되기 때문에 속도가 훨씬 빠르다.(GAN 짱짱맨)

 

_Nonlinear independent component analysis

명시적 density function을 사용하는 deep generative model의 또다른 종류는, 두 space에 대한 (input space / generative probability distribution의 space) continuous하고 nonlinear한 transformation에 기반한 방법이다.

예를 들어, latent variable z vector와 continuous, 미분가능 & invertible한 transformation g가 있다고 할때, g(z)는 x space로부터 샘플을 뽑아낼 수 있다.

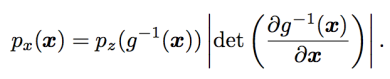
이 때 만약 pz가 tractable하고 g의 역함수의 Jacobian 행렬의 determinant가 tractable하다면, 이 px는 tractable하다. 다시 말해서, 1) z에 대한 간단한 distribution과 2) transformation g를 사용하면 x에 대한 복잡한 distribution의 space로 넘어갈 수 있게 되는 것이다. 그리고 g를 잘 디자인하면 x의 density도 구해버릴 수 있다.

이 방법의 가장 최근 모델은 NVP(Dinh et all, 2016) 모델이다.

(NVP 모델을 개인적으로 처음 접하기 때문에 간략한 설명을 첨부 :  Tractable한 학습, 샘플링, inference, evaluation을 위해, real-valued non-volume preserving (real NVP) transformation을 통해 모델의 space를 확장하는 방법. Real NVP는 powerful, stably invertible, learnable transformation 방법이란다.. 자세히는 향후에 봐야겠음. https://arxiv.org/abs/1605.08803 )

이러한  nonlinear ICA(independent component analysis) 모델의 단점은 function g에 대한 제한사항을 둔다는 것이다. 특히, invertibility가 필요한데 이는 latent z 가 x와 같은 dimensionality를 가져야 한다는 것을 의미한다. (GAN은 g에 대해 최소한의 requirement만을 요구하기 위해 디자인되었고, x보다 더 큰 dimension의 z를 허용한다. GAN 짱)

요약하자면, 명시적이고 tractable한 density를 정의하는 모델은 likelihood를 optimize하는데에 있어서 매우 효과적이지만, tractable한 density를 만들 수 있는 모델은 제한적이는 등의 단점들이 있다.

 

2_3_2 Explicit models requiring approximation

Tractable한 density function을 정의하기 어렵기 때문에, 명시적이긴 하지만 intractable한 density function을 정의한 후 approximation을 통해 likelihood maximization을 진행하는 모델들이 고안되었다. 이들은 크게 둘로 나뉜다.

• deterministic approximation을 사용하는 모델 (variational method)
• stochastic approximation을 사용하는 모델 (MCMC)

 

_Variational approximation

Variational method는 lower bound를 정의한다.

이 log-likelihood의 lower bound L을 maximize하도록 학습하는 것은 적어도 log-likelihood가 그만큼 높은 값을 얻는다는 것을 guarantee한다. 여러 모델들에서 computationally tractable한 L을 정의하는 것이 가능하다. (tractable한 log-likelihood를 정의하는 것은  불가능하더라도.)

현재까지 가장 popular한 방법은 VAE(variational autoencoder)이다.

Variational method의 단점은 너무 약한 appoximate posterior distribution 또는 너무 ‘약한’ prior distribution이 사용된다는 것이다. (여기서 약하다는 뜻은, 설사 infinite한 데이터로 optimize를 완벽히 한다고 해도, L과 true likelihood사이의 차이 때문에 p_model이 실제 p_data와는 달라질 수 있다는 뜻이다.)

이에 비해 GAN은 unbiased하도록 디자인되었기 때문에, 많은 데이터만 있다면 Nash 균형( (D와 G사이의)을 이룬 GAN으로 p_data를 정확히 재현할 수 있다. (GAN찬양 again)

사실 실제 사용할 때에는, variational method로 매우 좋은 likelihood를 얻을 수는 있지만 generate한 sample의 퀄리티가 떨어지는 편이다.  Sample의 퀄리티를 정량적으로 평가할 수 있는 방법은 없기 때문에 주관적이긴 하다.

VAE에서 sampling한 예이다. (아무래도 가우시안 prior 등에서 오기 때문에 blurry) 이와 비교해서 GAN이 만든 sample의 퀄리티가 어느면에서 더 좋다고 딱 집어서 얘기할 수는 없지만,(사실 딱 집어서 sharp하잖아…) 일반적으로는 더 좋다고 여겨진다.

FVBN에 비해서 VAE는 optimize하기 더 어렵다고 여겨지지만, GAN은 그렇지 않다.

 

_Markov chain approximation

대부분의 deep learning algorithm은 stochastic approximation을 사용한다. (적어도 minibatch를 뽑아서 loss 최소화에 사용하는 형태를 사용한다.)

Fair한 sample이 빠르게 generate될 수 있다면 (단순한 예를 들자면 training set에서 무작위로 추출), 보통 sampling-based approximation은 무리없이 잘 작동한다. Sample들간의 variance가 너무 높지만 않다면 말이다.

몇몇 모델들은 무작위 추출보다는 Markov chain 방식을 사용해서 좀더 expensive하게 sampling을 한다.

Markov chain은 x′∼q(x′|x) 라는 성질을 이용해서 반복적으로 sampling하는 방식이다. Transition operator q를 사용해서 x를 업데이트함으로써, Markov chain은 x가 결국 p_model(x)로부터 sampling되도록 converge한다.

하지만 이 convergence는 매우 느릴 수 있고, converge 했다는 완벽한 보장을 할 수도 없기 때문에, 실제 사용할 경우 너무 일찍(converge전에) x를 사용하게 되는 경우가 많다. (fair하지 않은 sample이 된다.)

또한 High-dimensional한 space에서는 Markov chain이 덜 효과적이다. Boltzmann machine은 training과  sample generation 모두에 Markov chain을 사용하는 모델이다. Boltzmann machine 은 deep learning 르네상스를 여는데 중요한 역할을 했지만, 이제는 거의 사용되지 않는데, 아마도 Markov chain approximation 부분이 큰 데이터셋을 처리하는 문제에는 활용되기 어렵기 때문일 것이다. (computation이 많으니까..)

게다가, training에 Markov chain method를 사용하는 것까지는 한다고 쳐도, sample generation에 사용하는 것은 single-step generation method에 비해서 매우 꺼려진다. (computational cost가 너무 크다.)

GAN은 Markov chain을 사용하지 않도록 디자인 되었다. 아하하..

몇몇 모델은 variational approximation과 Markov chain approximation 둘다를 사용하기도 한다. Deep Boltzmann machine 이 그 예이다.

 

2_4 Implicit density models

Density function이 명시적으로 정의되지 않고도 학습될 수 있도록 디자인된 모델들을 살펴보자.

이 모델들은 p_model과 간접적으로 interact함(sampling함)으로써 train되도록 설계되었다. 위에서 살펴본 taxonomy의 오른편 가지에 해당하는 모델들이다.

몇몇 모델들은 p_model로부터 sampling한 sample들에 기반해서 Markov chain transition operator를 정의한다. (converge하기 위해 어느정도 sampling을 해야함.) 대표적인 모델은 generative stochastic network이다. 하지만 2_3_2에서 살펴본 바와 같이 Markov chain은 high dimensional space의 데이터에서 사용이 어렵고 computational cost가 크다. GAN은 이 문제를 피할 수 있다.

마지막으로! (이 얘기하려고 여기까지 옴..)

가장 오른편에 있는 모델은(더 그레이트 GAN..) single step에 sampling을 바로바로 한다. 처음 GAN이 나올 때만 해도 이러한 종류로는 처음있는 모델이었지만, 이후 kernelized moment matching에 기반한 여러 추가적인 모델들이 발표되었다.

 

2_5 Comparing GANs to other generative models

요약해보자면, GAN은 다른 generative model들의 단점을 피하기 위해 고안되었다.

• FVBN이 x의 dimension에 비례한 runtime을 필요로 하는데 비해서, GAN은 sample들 병렬적으로(in parallel) 생성할 수 있다.
• Generator function을 디자인함에 있어 Boltzmann machine이 제약사항을 두는 것에 비해서 GAN은 제한 사항이 거의 없다. (Boltzmann machine에서는 tractable한 Markov chain sampling을 위해 사용할 수 있는 prob. distribution의 종류가 제한되어 있다.) 또한, Nonlinear ICA는 generator function이 invertible하고 latent z가 sample x와 같은 dimension을 가져야 하지만, GAN은 그렇지 않다.
• Markov chain이 필요치 않다. 이것은 Boltzmann machine과 Generative stochastic network에 비해 장점이다.
• Variational bound를 필요로 하지 않고, GAN framework에서 사용할수 있는 model의 종류들은 이미 universal approximator로 알려진 모델들이기 때문에 GAN은 점근적으로 consistent하게 된다. 몇몇 VAE들도 점근적으로 consistent하게 될 것이라고 추측되긴 하지만 증명되지는 않았다.
• GAN은 다른 방법들에 비해 더 나은(주관적으로) 결과물을 내어준다고 여겨진다.

하지만 GAN에게도 단점이 있다. Training할 때 (D와 G 사이의 game에서) Nash 균형이 필요하다. 이것은 objective function을 최적화하는 문제보다 더 어려운 문제이다.

 

3_ How do GANs work.

 

3_1 The GAN framework

GAN의 기본 아이디어는 2 player(Generator/Discriminator)간의 game을 설정하는 것이다.   Generator는 sample을 생성하는데, training data와 같은  distribution에서 생성되는 것을 목표로 한다. Discriminator는 생성된 sample들을 확인해서 이것이 실제 training data에서 온 것인지 만들어진 것인지 판별한다. Discriminator는 supervised learning으로 학습한다. (real / fake 두가지 class에 대한 학습) Generator는 discriminator를 속이도록 학습된다. 우리는 generator를 위조지폐를 만드는 자라고 볼 수 있고 discriminator를 이를 잡아내려는 경찰이라고도 볼 수 있다. 이 게임에서 이기기 위해서는, 위조자는 실제 지폐와 구별되지 않는 지폐를 만들기 위해 노력할 것인데, 이처럼 generator는 마치 training data의 distribution에서 나온 sample들과 같은 sample들을 만들어내도록 학습될 것이다.

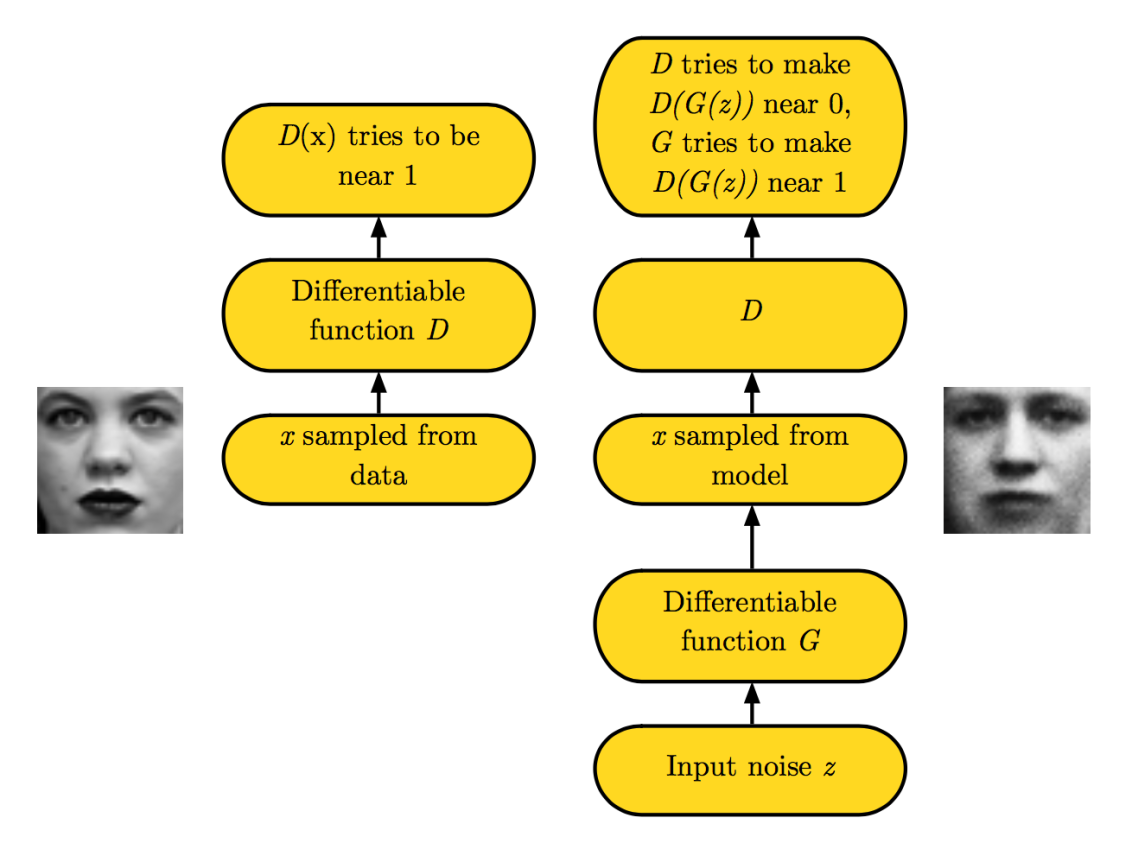
모델의 structure를 보자면, GAN은 latent variable z와 observed variable x를 포함하는 structured probabilistic model이라고 볼 수 있다. Graph structure는 다음과 같다. (매우 단순..)

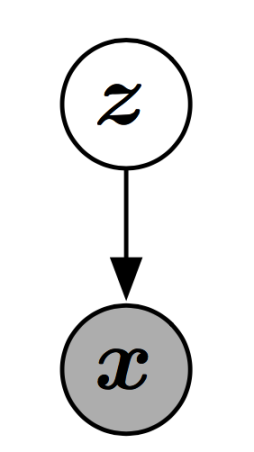
두 player들은 2개의 function으로 나타내는데, 각각 function은 자신의 input과 parameter들에 대해서 미분가능하도록 한다.(neural net) Discriminator는 x를 input으로 받고 Θ^(D)를 parameter로 사용하는 function D로 정의한다. Generator는 z를 input으로 받고 Θ^(G)를 parameter로 사용하는 function G로 정의한다.

각 player는 양쪽 player 모두의 parameter들로 정의된 cost function을 갖는다.

Discriminator 는 J_(D)(Θ^(D), Θ^(G))를 최소화하고자 하는데, 오직 Θ^(D)를 업데이트 함으로써 이를 달성하고자 한다.

Generator 는 J_(G)(Θ^(D), Θ^(G))를 최소화하고자 하는데, 오직 Θ^(G)를 업데이트 함으로써 이를 달성하고자 한다.

각 플레이어의 cost가 상대방의 parameter에 영향을 받는데, 서로 상대방의 parameter는 제어할 수 없기 때문에, 전체 모델은 optimization 문제라기 보다 하나의 game이 된다.

Optimization문제의 해는 parameter의 space에서 (local) minimum의 지점(주변의 모든 point들이 더 큰 cost를 갖는)이 된다.

하지만 game문제의 해는 Nash 균형이다. 여기서 우리는 local differential Nash equilibria이라는 term을 사용한다. Nash 균형은, Θ^(D)에 대한 J^(D)의 local minimum과 Θ^(G)에 대한 J^(G)의 local minimum을 만족하는 (Θ^(D), Θ^(G)) tuple을 의미한다.

 

_The generator

Generator는 단순히 어떤 미분가능한 함수 G이다. (neural net)

z가 어떤 simple한 prior distribution으로부터 샘플링되었을 때, G(z)는 p_model로부터 나온 x의 sample을 생성하게 된다는 개념이다. (우리가 원하는 바)

일반적으로, G는 deep neural network로 구성한다. 함수 G의 input은 꼭 deep neural network의 첫 레이어의 input일 필요는 없다. G의 input은 전체 네트워크의 어느 부분이든 들어가면 된다.

예를 들어, 우리는 z를 두개의 vector z⁽¹⁾과 z⁽²⁾로 나누어서 z⁽¹⁾을 첫번째 레이어의 input으로 넣고 z⁽²⁾를 마지막 레이어의 인풋으로 넣을 수도 있다. 만약 z⁽²⁾가 Gaussian이었다면, 이는 x를 conditionally Gaussian(given z⁽¹⁾)하게 만든다.

또다른 인기있는 방식은 additive또는 multiplicative noise를 hidden layer에 적용하거나, concatenate 시키는 것이다.

전체적으로 보자면, generator net을 디자인함에 있어서 별다른 제약사항은 없다고 볼 수 있다. 단지 p_model이 x space를 온전히 지원하길 원하면, 우리는 z의 dimension이 적어도 x의 dimension만큼의 크기를 갖도록 해야 한다. 또한 G는 미분가능해야 한다. 이 두가지가 유일한 제한사항이라고 볼 수 있다.

특히, nonlinear ICA 방식으로 train할 수 있는 모델이라면 무엇이든 GAN의 generator network가 될 수 있다.

VAE와의 관계는 좀 더 복잡하다. 어떤 경우엔 GAN framework로 VAE가 train할 수 없는 모델들을 train할 수 있고, 반대의 경우도 존재한다. 하지만 이 두 framework가 공유하는 부분도 크다.(둘다되는 부분)

이 둘의 가장 두드러지는 차이점은, VAE는 standard한 backpropagation을 통해서는 discrete variable을 generator의 인풋으로 가질 수 없다는 것이고(VAE의 generator(decoder)의 인풋은 distribution function), GAN은 discrete variable을 generator의 아웃풋으로 가질 수 없다는 것이다.

 

_Training process

Training process는 동시에 일어나는 SGD로 구성된다.

매 step마다 두개의 minibatch가 먼저 샘플링된다. (dataset으로부터 얻은 x 값의 minibatch / prior로부터 얻은 latent z의 minibatch)

그리고는 두개의 gradient step이 동시에 일어난다.

• J^(D)를 감소시키는 방향으로  Θ^(D)만을 업데이트하는 gradient descent
• J^(G)를 감소시키는 방향으로 Θ^(G)만을 업데이트하는 gradient descent

두 경우 모두 gradient-based optimization을 사용하는 것이 가능하다. (Adam, RMSProp 등)

원래 두개중 하나에 더 많은 step을 update하는 방법들을 사용했지만, 2016년말 현재 저자의 주장에 따르면 동시에 한번씩 업데이트하는 것이 실제로 가장 잘 작동한다고 한다.

 

3_2 Cost functions

3_2_1 Discriminator의 cost J^(D)

GAN을 위해 디자인된 여러 방식의 game들이 있지만, 모두 같은 J^(D)를 사용한다. :

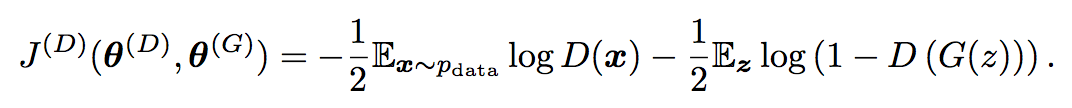
이 식은 사실 sigmoid output을 갖는 기본적인 binary classifier에 대한 cross-entropy cost 수식이라고 볼 수 있다.(사실 binary classifier이니까..) 한가지 차이점은 classifier가 두개의 minibatch에 대해서 train된다는 것이다. (dataset으로부터 온 minibatch(label이 모두 1) / generator로부터 온 minibatch(label이 모두 0))

모든 GAN버전들은 위 식을 최소화하도록 discriminator를 독려한다. 모든 경우에discriminator는 같은 strategy를 갖는다.

Discriminator를 train함으로써 우리는 모든 x point에 대해서 다음 ratio에 대한 estimate를 구할 수 있다. :

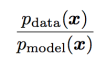
이 ratio를 estimate함으로써 우리는 다양한 종류의(다양한 GAN의) divergence와 그에 대한 gradient를 구할 수 있다. (이것이 GAN을 VAE나 Boltzmann machine과 구별하는 핵심 approximation 테크닉이다.)

즉, 다른 deep generative model들은 lower bound나 Markov chain에 대한 approximation을 구하지만, GAN은 이 두 density의 ratio에 대한 supervised learning에 기반한 approximation을 구하는 것이다.

GAN approximation은 supervised learning이 성공하느냐의 여부에 달려 있다. (overfit 또는 underfit이 일어나면 approximation도 실패라고 볼 수 있음) 원칙적으로는, 많은 양의 데이터와 완벽한 optimization이 된다면, 이같은 실패는 극복될 수 있다.

GAN말고 다른 모델들은 다른 실패요인들을 갖고 있으니 GAN만의 문제는 아니다(..)

GAN framework을 game이론의 도구들을 사용해서 분석할 수 있기 때문에 우리는 GAN을 ‘adversarial’이라고 부르는 것이다. 하지만 사실 이 둘이 cooperative하다고도 볼 수도 있다. Discriminator가 density들의 ratio를 estimate한 뒤에 generator에게 그 정보를 공유하기 때문이다. (..) 이같은 관점에서, discriminator는 어떤 의미에서 generator를 가르치는 선생이라고도 볼 수 있다. 이 같은 관점의 전환은 사실 뭐 큰 의미는 없다. (..)

3_2_2 Minimax

지금까지 우리는 discriminator를 위한 cost function을 정의했다. 이제 generator의 cost function을 살펴보자.

‘Game’의 가장 단순한 버전은 zero-sum game이다. (모든 플레이어의 cost의 합이 항상 zero가 되는 것) 우리 게임에 적용하자면, J^(G) = – J^(D) 이라고 할 수 있다.

J^(G)가 J^(D)와 직접적으로 연결되어 있기 때문에, 우리는 전체 game을 하나의 value function으로 정의해서 discriminator의 cost를 정의할 수 있다.

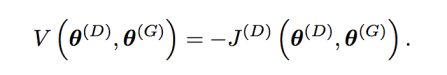
이 zero-sum game은 minimax game이라고도 불린다. 이 문제의 해는 바깥 loop을 최소화하고 안쪽 loop을 최대화하는 두가지를 모두 포함하기 때문이다.

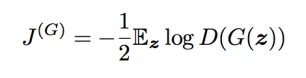
이 minimax game은 이론적으로 분석해볼 수 있기 때문에 흥미로운 주제이다.

Goodfellow는 이같은 GAN game의 변형을 사용해서 이 game의 학습과정이 실제 data의 distrbution과 모델 distribution간의  Jensen-Shannon divergence 를 최소화하는 것과 유사하다는 것을 보였다. 즉, 두 플레이어의 policy가 해당 function의 space에서 바로 update될 수만 있다면 game은 균형상태로 converge한다는 뜻.

하지만 실제 사용예에서는, ‘플레이어’들은 deep neural network로 구현되고, update는 parameter space에서 일어나기 때문에 convexity를 전제로 하는 이같은 결과(균형)를 적용하기는 어렵다.

3_2_3 Heuristic, non-saturating game

앞서 본 generator에 대한 cost(J^(G) = – J^(D))는 이론적인 분석을 가능하게 하지만, 실제 사용시에는 적용되기 어렵다.

Target class와 classifier의 predicted distribution 사이의 cross-entropy를 최소화하는 것은 매우 효과적이다. (classifier가 틀린 아웃풋을 내었을 때 cost가 절대 saturate하지 않기 때문에)

Minimax game에서 discriminator는 cross-entropy를 최소화하지만, generator가 같은 cross-entropy를 최대화한다. Discriminator가 generator의 sample들을 잘 reject하게 되면  generator의 gradient는 결국 vanish하게 되고, 이때는 결국 cost가 saturate하게 된다.(0을 향해..)

-> 이 문제를 해결하기 위한 한가지 방법은, generator에 대한 cross-entropy minimization을 계속해서 사용하는 것이다. : Discriminator의 cost에 대해 부호를 뒤집어서 generator의 cost를 구하는 대신, cross-entropy를 만들기 위한 target의 부호를 뒤집는다. 그렇게 하면 generator의 cost는 다음과 같이 된다. :

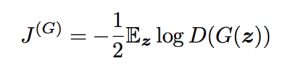
 Minimax game에서 generator는 discriminator가 옳게 판단할 log-probability를 최소화하려고 한다. (즉, generator는 discriminator가 실수할 확룔을 높이고자 한다.)

이 버전의 게임은 이론적으로 정리된다기 보다는 휴리스틱하게 정의될수 있는 것이다. 각 플레이어는 게임에서 ‘지고 있을 때’ 강한 gradient를 갖게 되도록 하는 것이 이 버전의 한가지 목표가 된다.

이 버전은 더이상 zero-sum 게임이 아니게 되고, 하나의 value function으로 정의될 수 없게 된다.

3_2_4 Maximum likelihood game

우리는 GAN에 Maximum likelihood learning을 적용하고 싶을 수도 있다. 이는 data와 model사이의 KL divergence를 최소화하는 것을 의미한다. 사실 그에 앞서서, GAN에 부차적으로 maximum likelihood를 적용할 수도 있다고 살펴보았다. (다른 모델들과 단순하게 비교하기 위해)

GAN framework 안에는 approximate를 위한 여러가지 종류의 수식이 있다. Goodfellow는, 만약 D가 이미 optimal 하다면, 다음과 같은 수식을 사용하는 것이 KL Divergence의 parameter를 minimizing하는 것과 같다는 것을 보였다.

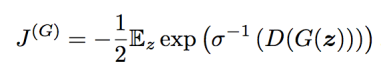
(σ는 logistic sigmoid function)

이 cost를 최소화하는 것 => 이는 다음 식의 D_KL를 최소화하는 것과 같음.

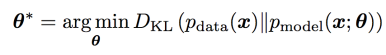
실제 사용예에서는, KL divergence에 대한 stochastic gradient descent (x 샘플)와 GAN의 training 과정(z 샘플)에서 샘플링을 사용하기 때문에(그렇기 때문에 estimated gradient이다) true expected gradient 부근에서 약간의 variance를 가질 것이다.

참고로, GAN framework 내부의 maximum likelihood를 approximate하는 다른 방법도 있다. (Training generative neural samplers using variational divergence minimization.  Nowozin et al. (2016) 논문 참고)

3_2_5 Is choosing the divergence distinguishing in GAN? (divergence종류의 차이가 GAN의 훌륭한 output의 이유가 되는가?)

GAN이 어떻게 작동하는지 살펴보는 일환으로, 정확히 무엇이 sample generation에서 효과적으로 작동하는지를 살펴보자.

예전엔, 많은 사람들이 GAN이 Jensen-Shannon divergence룰 사용하기 때문에 sharp하고 realistic한 sample을 만들어낸다고 생각했다. (VAE가 data와 model의 distribution들간의 KL divergence를 최소화하는 데에 비해)

KL divergence는 symmetric하지 않다. (D_KL(p_data|p_model) ≠ D_KL(p_model|p_data)) Maximum likelihood estimation은 D_KL(p_data|p_model)를 사용한다. 그에 비해 JS divergence는 D_KL(p_model|p_data)를 사용한다고 볼 수 있다.

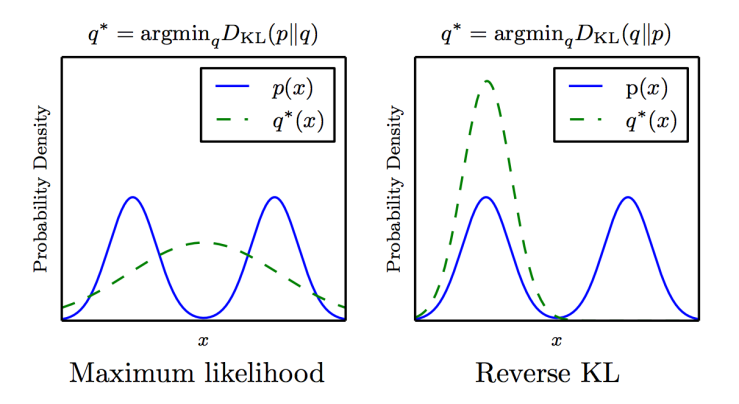
위 그림을 보면 알 수 있듯이 D_KL(p_model|p_data)를 사용하는 것이 좀 더 정확한 sample을 만들어 낸다. 이 KL divergence로 학습된 모델은 오직 training distribution으로부터 온 sample만을 generate하도록 학습되었기 때문이다.

(1-dimensional x에 대한 GMM 모델에 대해서 q를 학습한 결과. : Single 가우시안인 q로는 정확히 재현할 수 없지만, 어떤 divergence를 선택하느냐에 따라서 만들어지는 q의 모습이 달라지는 것을 볼 수 있다. 왼편의 maximum likelihood 방법은 두 mode를 average하는 타협점으로 학습하게 되고, 오른편의 reverse order KL divergence를 사용한 방법은 두 mode중 한개를 선택해서 학습하게 된다.(둘 중 다른 mode를 선택할 수도 있다. 두 mode가 모두 reverse KL divergence의 local minima이기 때문.)

즉,

• D_KL(p_data|p_model)는 data가 나타나는 모든 range에서 높은 확률을 얻기를 원하는 방식으로 학습되고,
• D_KL(p_model|p_data)는 data가 나타나지 않는 부분에서 낮은 확률을 얻기 원하는 방식으로 학습되는 것이다.

이같은 관점으로 보면, D_KL(p_model|p_data)은 unusual한 샘플을(distribution의 mode들 사이에서) 만들어내지 않으려 하기 때문에 더 보기 좋은 sample을 만들어낸다고 볼 수 있다.

즉, 모든 mode를 포함하는 것보다 차라리 몇몇 mode를 무시하는 편이 unusual하지 않은 샘플링을 하기 위해서는 효과적이라는 뜻.

하지만 최근의 연구에서는 JS divergence를 사용하는 것이 GAN의 좋은 결과의 이유가 되지 않는다는 증거를 찾기도 했다.

• 어떤 모델에서는 GAN이 maximum likelihood game으로도 학습될 수 있다는 것을 보였다. (그러면서도 여전히 몇개의 mode만을 선택하여 sharp한 output을 내어준다.) : f-GAN은 여러 종류의 divergence를 사용할 수 있었음. / D_KL(p_data|p_model)도 몇개의 mode만을 선택해서 sharp한 sample을 뽑아냄.
• GAN은 적은 수의 mode들만을 선택하는 경향이 있다. (model의 capacity에 의해 제한된 수보다 더 적은 수) Reverse KL은 model이 제공해줄 수 있는 가능한한 많은 수의 mode를 사용하려고 한다.(일반적으로는 적은 수의 mode를 선호하지 않음) 이는 mode collapse가 divergence의 종류에 따른 것이 아닌 것임을 보여준다.

따라서, GAN은 divergence의 성격 때문이 아니라 트레이닝 과정에서 있는 어떤 ‘결함’ 때문에 적은 수의 mode를 선택한다고 볼 수 있다. Mode collapse에 대해서는 후에 다시 다루기로 하겠지만, GAN을 사용해서 학습된 mode들의 family가 VAE를 사용해서 학습된 mode들의 family와 다르기 때문이라고 볼 수 있다.

예를 들어, GAN을 사용했을 경우, isotropic(등방) Gaussian(generator의 input에 의해 condition된)을 사용하는 것보다 더 복잡한 distribution을 갖는 x을 generate하는 모델을 만들기가 더 수월하다.

혹은 GAN이 사용하는 approximation이, 다른 framework들이 사용하는 것과는 다른 effect를 갖고 있기 때문일 수도 있다.

 

3_2_6 Comparing cost functions

GAN의 generator network는 사실 강화학습의 이상한(?) 형태라고도 볼 수 있다.  각 z에 최적화된 특정 x가 아웃풋으로 주어진다기 보다는, 어떤 액션을 취하고 그에 따른 보상을 받는다는 측면에서 그러하다.

특히 GAN의 J^(G)는 training data에 직접 접근하지 않고, training data에 관한 모든 정보를 discriminator로 부터 전달받는다. (부수적으로,  이같은 점이 overfitting을 막아주기도 한다. Generator가 training data를 직접 copy할 기회가 없어지기 때문이다.)

하지만 전통적인 강화학습과는 사실 다른데,

• Generator가 reward function의 output만을 보는 것이 아니라 gradient도 보고,
• Reward function은 stationary하지 않다. Reward는 generator의 policy 변화에 따라 대응하는 discriminator에 따르기 때문이다.

모든 경우, 우리는 하나의 z에 대해서 sampling하는 과정이 어떤 reward를 받는 에피소드라고 볼 수 있다. (다른 z에 대한 action에 independent한) 여기서 Reward는 하나의 scalar값에 대한 function이다. : D(G(z))

이것을 cost 개념으로 볼수 있다. Generator의 cost는 D(G(z))에서 항상 단조 감소하지만, game을 다르게 디자인하면 curve의 여러부분에서 이 감소 속도를 빠르게 할 수 있다.

다음 그림은 GAN의 3가지 변형에 대한 D(G(z))의 여러 함수들의 cost response curve를 나타낸다.

Maximum likelihood game이 cost에서 가장 높은 variance를 보이는 것을 볼 수 있고,  이 cost gradient의 대부분이 몇몇의 z(‘most likely to be real rather than fake’한)로부터만 온 것임을 알 수 있다.

휴리스틱하게 디자인된 non-saturating cost는 낮은 sample variance를 보이는데, 이로 인해 실제 사용할 때 더 나은 결과를 나타낸다고 볼 수 있다.

이는 variance를 감소시키는 기법이 GAN의(특히 maximum likelihood 기반의 GAN의) 성능을 향상시키는 중요한 연구주제임을 알려준다.

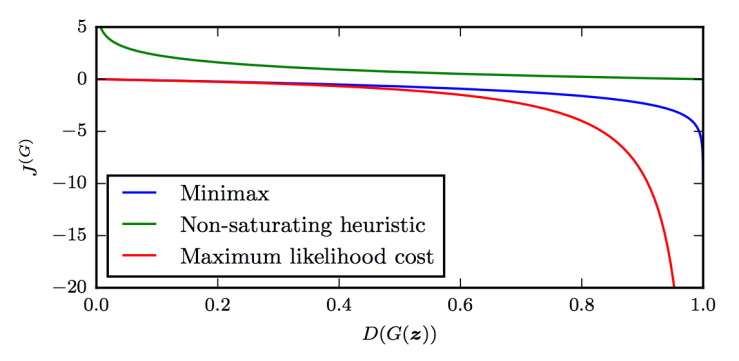
(그림의 non-saturating heuristic 부분에 대해 정확히 이해하지 못함. 나중에 다시 보자.)

 

3_3 DCGAN architecture

대부분의 GAN모델은 DCGAN architecture에 기반한다. (Deep convolutional GAN)

DCGAN의 특징은 다음과 같다.

• Batch normalization 을 generator와 discriminator의 대부분의 레이어에서 사용한다. (discriminator에 사용하는 두 minibatch에 각각 따로 적용) Generator의 마지막 레이어와 discriminator의 첫 레이어는 batch normalization이 적용되지 않는데, 모델이 data distribution에 대한 정확한 mean과 scale을 학습해야 하기 때문이다.
• 전체 네트워크 구조는 all-convolutional net 으로부터 가져온 것이다. 이 architecture는 pooling 이나 unspooling 레이어를 사용하지 않는다. Generator가 spatial dimension을 증가시킬 필요가 있을 때에는, transposed convolution(1보다 큰 stride 사용)를 대신 사용한다.
• SGD with momentum보다는 Adam optimizer를 사용한다.

DCGAN 이전에는 LAPGAN으로만 high resolution image를 다룰 수 있었다. LAPGAN은 multi-stage generation process를 필요로 한다. (이미지의 Laplacian pyramid representation의 각 level을 generate하는) DCGAN은 한번에 high resolution image를 generate하는 첫 GAN 모델인 셈이다.

제한된 도메인의 이미지에 대해서 DCGAN은 매우 높은 퀄리티의 이미지를 generate해준다. 또한 DCGAN은 GAN이 latent code를 유의미하게 사용하는 방법을 배웠다는 것을 보여준다. (latent space에서의 간단한 사칙연산으로 이미지의 semantic한 특성들에 대한 operation을 가능함을 보여줬다.)

(유명한 사진..)

3_4 GAN을 noise-contrastive estimation, 그리고 maximum likelihood와 어떻게 비교할 수 있을까?

GAN의 작동방식을 이해하기 위해서, noise-contrastive estimation(NCE)와 어떤 식으로 연관성이 있는지 살펴보자. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models.(Gutmann and Hyvarinen, 2010)

* 잠깐 NCE를 살펴보고 가자. Observed data와 generated noise(어떤 fixed noise임) 사이의 nonlinear logistic regression을 적용하는 모델이다. (Regression nonlinearity에는 model log-density function을 사용) 이 모델은 parameter에 대해 consistent(converge하는) estimator을 도출하게 되고, 점근적인 variance를 도출한다. 특히, 적분해서 1이 되지않는 unnormalized한 density function을 갖는 model들에도 바로 적용할 수 있다.

Click to access gutmann10a.pdf

Minimax GAN은 NCE의 cost function을 value function으로 사용하기 때문에 표면적으로 매우 관련성이 높을 것 같지만, 둘은 학습과정에서 다른 것들을 학습한다. (game안에서 각기 다른 player에 초점을 맞추기 때문)

러프하게 보면, NCE의 목표는 discriminator의 density model을 학습하는 것인 반면, GAN은 sampler(generator)를 학습하는 것이다. 이 두가지 task가 매우 밀접해보이지만, 사실 둘의 gradient는 매우 다르다.

놀랍게도, maximum likelihood는 NCE와 매우 유사하고, 같은 value function을 사용하여 minimax game을 진행한다. 하지만 플레이어에게 gradient descent보다 어떤 휴리스틱한update strategy를 사용한다는 점이 다르다.

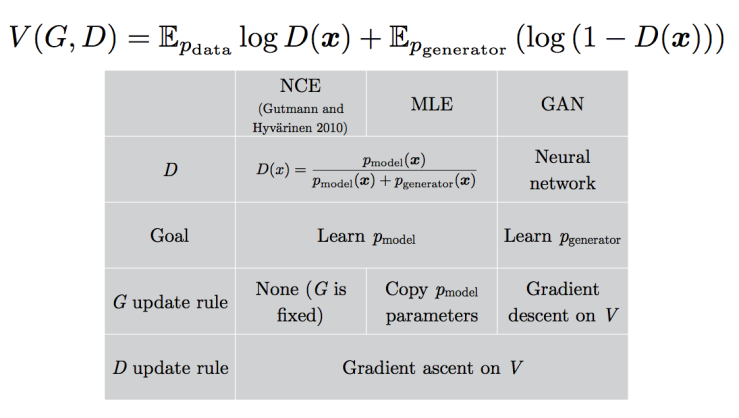
_?  Generator의 목적이 ratio에 대한 MLE를 무조건 높이는 게 아니라 0.5가 되도록 하는 게 아닌가? 라는 질문

 

4_ Tips and Tricks

GAN을 실제로 사용할 때 성능을 높이기 위한 팁들을 살펴보자. 몇몇 트릭들이 얼마나 효과적인지 사실 정확히 입증하긴 어렵다. (다른 부분을 손상하면서 성능을 높이기도 한다.) 따라서 한번쯤 시도해볼만 하다는 정도로 여기는 것이 옳다.

4_1 Train with labels

어떤 모양이나 형태로든, 레이블을 사용하는 것은 매우 드라마틱한 성능 개선을 보여준다. (물론 아웃풋에 대한 주관적인 평가 시에)

이 방법은 class-conditional GAN에서 처음 사용되었는데, class에 특정되지 않은 sample을 만드는 기존 GAN보다  훨씬 나은 결과물 보여주었다. (https://arxiv.org/abs/1506.05751)

Improved Techniques for Training GANs 논문에서는 (https://arxiv.org/abs/1606.03498) discriminator의 트레이닝 과정에서 object의 class를 구분하도록 하기만 하면, generator의 sampling 시점에 class 정보를 명시적으로 지정하지 않아도 여전히 나은 결과물을 내어준다는 것을 발견했다.

(*참고 코드 : https://github.com/openai/improved-gan)

이런 트릭이 왜 좋은 결과를 내어주는지는 사실 명확치 않다. Class 정보를 맵핑해 주는 것이 optimization과정에서 무언가 도움을 주기 때문일 수도 있다. 또한, sample quality에 대해서 객관적인 개선효과를 주는 것이 아니지만, 인간이 사물을 보는 특성에 더 가깝도록 sample을 bias시키는 효과를 주는 것일 수도 있다.

후자의 효과가 사실이라면, 사실 ‘true’ data-generating distribution에 대한 모델링으로서는 좋은 결과를 내어주는 게 아닐 수도 있다.

하지만 여전히 이런 트릭들은 사람에게 보기 좋은 미디어를 생산하는데에 효과적이고, 강화학습에 사용한다면 agent가 사람의 시각을 좀 더 반영한 환경에 대한 학습을 수행하는데에 좀 더 효과적으로 사용될 수 있을 것이다.

따라서, 여러 모델을 비교한다고 했을 때, 한 모델에 Label을 사용하는 트릭을 사용했으면, 다른 모델에도 같은 트릭을 사용해서 학습시켜야 한다. (동등한 조건으로 비교해야 한다.) Label 트릭의 사용여부 유무는 마치 convolutional model과 non-convolutional model의 차이 정도의 명백한 차이를 지닌다.

4_2 One-sided label smoothing

GAN은 discriminator가 두 density 사이의 ratio를 estimate함으로써 작동하게 모델링되어 있따. 하지만 deep neural net은 어떤 correct한 class에 대한 매우 높은 확률을 만들어 냄으로써 confident한 classification을 수행하도록 학습되는 경향이 있다. 이런 경향은 deep network의 인풋이 adversarially construct되었을 경우 더 강하다. (classifier가 linear하게 추론하고 매우 확신에 찬 prediction을 하는 경향이 있다.)

따라서 discriminator가 좀 더 소프트하게 estimation을 수행할 수 있도록 하기 위해, one-sided label smoothing 이라는 테크닉을 사용한다.

앞서 봤듯이 discriminator는,

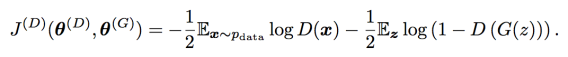
이 식을 통해 학습시킨다.

이것을 tensorflow 코드로 구현하면 다음과 같다. :

 d_on_data = discriminator_logits(data minibatch) d_on_samples = discriminator_logits(samples minibatch) loss = tf.nn.sigmoid_cross_entropy_with_logits(d_on_data, 1.) + tf.nn.sigmoid_cross_entropy_with_logits(d_on_samples, 0.) 

One-sided label smoothing의 기본 아이디어는, true label의(real 데이터에서부터 왔다는 판단) 타겟값을 1보다 약간 작은(0.9 같은) 값을 갖도록 하는 것이다.

 loss = tf.nn.sigmoid_cross_entropy_with_logits(d_on_data, .9) + tf.nn.sigmoid_cross_entropy_with_logits(d_on_samples, 0.) 

이렇게 함으로써 discriminator의 extreme한 extrapolation을 예방할 수 있다. 만약 discriminator가 어떤 인풋에 대해 매우 큰 logit 값을(1에 가까운 확률) 예측하도록 학습된다면, logit 값을 낮추도록 penalize되는 것이다.

Fake sample에 대해서는 label을 smoothing하지 않는 것이 중요하다.

예를 들어,  real data에 대해서 1 – α 를 타겟 값으로 설정하고, fake sample에 대해서 0 + β를 타겟값으로 설정했다고 하자. 그러면 optimal한 discriminator function은 다음과 같다. :

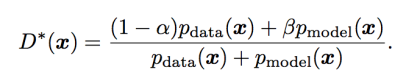
β가 0일 경우, α로 smoothing한다고 해도 optimal value를 scale down하는 결과만을 가져온다. 하지만 β가 0이 아니라면, optimal discriminator function의 shape이 달라진다.

특히, p_data(x)가 매우 작고 p_model(x)가 매우 큰 경우(영역)에는, D*(x)는 p_model(x)의 잘못된(spurious한) mode 근처에서 피크를 보일 것이다. 따라서 discriminator는 generator에게 잘못된 정보를 주게 된다. : generator는 data와 비슷한 sample을 만들거나 전에 만든(지금 만들고 있는) sample과 비슷한 sample을 만들도록 학습될 것이다.

One-sided label smoothing은 사실 오래된(1980년대) smoothing  테크닉의 간단한 modification이다. Rethinking the Inception Architecture for Computer Vision 논문은(https://arxiv.org/abs/1512.00567) label smoothing 이 object recognition문제에서 convolutional network의 훌륭한 regularizer임을 보였다. 그 이유는 1) 모델이 incorrect한 class를 선택하지 않도록 하는 범위에서 2) correct한 class에 대한 확신을 줄여주기 때무이다. 다른 (Weight decay같은) regularizer는 coefficient가 너무 높게 설정되면 misclassification을 하도록 할 위험이 있다.

Adversarial Perturbations Against Deep Neural Networks for Malware Classification논문에서는 (https://arxiv.org/abs/1606.04435) label smoothing이 adversarial 예제들의 약점을 보완한다고 보였다. (discriminator가 generator의 공격에 대응하는 법을 좀 더 효과적으로 배우도록 함으로써)

 

4_3 Virtual batch normalization 

DCGAN이 소개된 이후로, 대부분의 GAN architecture들은 batch normalization을 어떤 형태로든 사용했다.

Batch normalization은 모든 레이어에서 (feature를 뽑아내기 위한) weight값들 사이에 복잡한 인터랙션이 이루어져야 하는 부분을 개선해서, 모든 feature에서 하나의 mean과 하나의 variance값을 갖도록 reparameterize하는 것이다. 이로써 모델의 optimization 결과를 개선한다.

이런 reparametrization은 한 minibatch마다 각 feature에서 mean 값을 빼고 variance값으로 나누어 줌으로써 이루어진다.

이러한 normlization이 해당 모델의 일부분이 되는 것이 중요하다. 왜냐하면, Back propagation이 항상 normalize되도록 정의된 gradient를 계산해야 하기 때문이다. 모델의 일부분으로 normalization이 이루어지도록 하지 않고 feature들이 그저 자주 normalized되도록 하면 덜 효과적이 된다.

Batch normalization은 매우 도움이 되는 방법이지만, GAN에서는 불행히도 안좋은 side effect가 있다. 매 스텝마다 다른 minibatch를 사용하면서 normalization을 계산하도록 하면 normalizing constant에 불안정한 요동이 일어나기 때문이다.  Minibatch의 크기가 작을 경우 (주로 GPU memory가 작은데 커다란 generative 모델을 학습하려고 할 경우), 이런 요동함이 매우 클 수 있고, 따라서 GAN이 생성하는 이미지가 z보다 이런 fluctuation에 의해 더 영향을 받을 위험이 있다.

위 이미지가 그러한 예시이다. Batch normalization으로 인한 fluctuation이(각 feature의 mean과 standard deviation 값의 fluctuation) 각 z code의 영향력보다 커진 경우이다. 한 minibatch는 orange 색 위주의 샘플들만을 포함하고, 다른 minibatch는 green색 위주의 샘플들만 포함하고 있는 경우였다. 이들은 사실 서로 독립적이었어야 하지만 batch normalization 때문에 서로간의 correlation이 생겨버렸다.

Improved techniques for training gans 논문에서 (https://arxiv.org/abs/1606.03498) 이문제를 완화하는 방법을 제시했다. Reference batch normalization이라는 방법인데, 네트워크를 두번 통과하는 방식이다. 학습 맨 처음 한번은 reference example을 샘플링해서 mini batch로 통과시킨다. (이는 이후 교체되지 않는다.) 그리고 또 한번은 원래 방식으로 샘플링한 이번 스텝의 minibatch를 통과시킨다. Mean과 standard deviation값은 reference minibatch에서 얻었던 값을 계속해서 사용한다. (두 batch들의 feature는 이 값을 가지고 normalize된다.)

하지만 이 방법의 결점은 모델이 reference batch에 overfit될 수 있다는 점이다. 이 문제를 완화하기 위해서 virtual batch normalization이라는 방법을 사용한다. 이는 각 샘플을normalizing하기 위한 값을 그 샘플과 reference batch의 union을 사용해서 얻어낸다. Reference batch normalization과 virtual batch normalization 둘다, minibatch안의 모든 샘플들이 서로에 대해 독립적으로 process된다는 특징을 갖는다. 또한, generator가 생성하는 샘플들도 모두 서로간에 i.i.d하다. (reference batch를 정의하는 샘플들만 제외하고)

 

4_4 G와 D의 밸런스를 맞출 수 있을까??

G와 D 중 어느 하나가 다른 하나를 제압해버리지 않도록 어떻게든 밸런스를 맞추는 것이 필요하다고 많은 연구자들이 직관적으로 생각해왔다. 이런 밸런스가 필요하고 또 실현 가능하다면, 주목할만한 방식으로는 아직 소개되지 않았다.

GAN의 저자는 data density(pdf)와 model density(pdf)의 ratio를 측정함으로 GAN이 동작한다고 (현재까지는) 믿고 있다. 이 ratio는 discriminator가 optimal해졌을 때에만 정확히 측정되므로, discriminator가 generator를 제압해버리는 것은 괜찮다고 볼 수 있다.

• Discriminator가 너무 정확해지면, 때때로 generator의 gradient가 vanish해버릴 수 있다. 하지만 이 문제를 해결하기 위한 방법은 discriminator의 능력을 제한하는 것이 아니라, gradient가 vanish하지 않도록 game을 잘 parameterization하는 것이다. (섹션 3.2.3 Heuristic, non-saturating game 참고)
• Discriminator가 너무 확신을 가지게 되어 버리면,  generator의 gradient는 때때로 너무 커져버릴 수도 있다. 이럴 때 discriminator의 정확도를 낮추는 것보다는 one-sided label smoothing을 하는 것이 좋다. (섹션 4.2 참고)

Ratio를 잘 예측하기 위해서는 discriminator는 항상 optimal해야 한다는 아이디어는 generator가 한번 학습될 때마다  discriminator를 한번 이상 학습시키는 방식을 제시한다. 하지만 실제 학습시에는 이 방식이 그다지 성능 개선을 가져다 주지 않는다.

모델 사이즈를 다르게 함으로써 G와 D의 밸런스를 맞추는 방법도 시도해볼 수 있다. 실제 상황에서는, D는 보통 더 깊고 각 레이어에 더 많은 수의 필터를 가지도록 한다.

이는 D가 (두 density의 ratio를) 정확히 예측하는 것이 중요하기 때문일 것이다. 하지만 이 방식 역시 mode collapse 문제라는 부작용이 있을 수 있다. G는 현재의 학습 방식으로 본인의 전체 capacity를 다 사용하지 않으려는 경향이 있기 때문에, 실제 실험자들은 G의 capacity를 늘리는 것으로는 딱히 이득을 얻지 못한다고 추정한다.

만약 mode collapse 문제가 극복 가능하다면, G의 크기는 아마 더 커질 것이다. (D의 크기도 그에 비례해서 커질 것인지는 명확하지 않다.)

5 Research  Frontiers

다음 포스팅에 이어서..